












6.7. Ортогональные системы кусочно-постоянных функций
Кусочно-постоянной называют функцию, сохраняющую неизменное значение на заданном множестве интервалов. Формально ее можно определить как
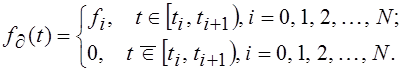
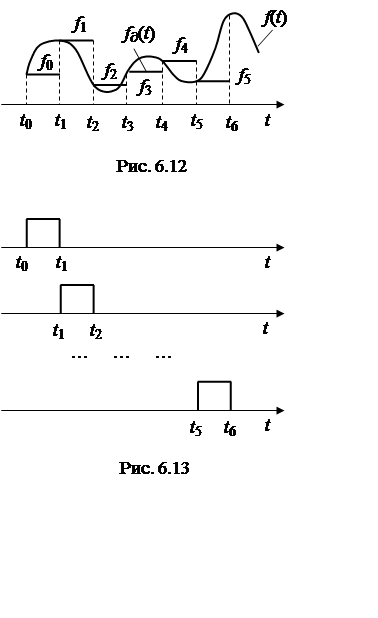
На рис. 6.12 приведен график кусочно-постоянной функции для ![]() и функции
и функции ![]() , из
которой она получена путем запоминания (сохранения) значения
, из
которой она получена путем запоминания (сохранения) значения ![]() в пределах промежутка
в пределах промежутка ![]() .
.
 Таким образом, множество чисел
Таким образом, множество чисел ![]() и
и ![]() полностью
определяет функцию
полностью
определяет функцию ![]() .
.
Обычно моменты времени ![]() (моменты дискретизации временной шкалы)
берутся через одинаковые промежутки времени
(моменты дискретизации временной шкалы)
берутся через одинаковые промежутки времени ![]() (интервал
дискретизации), согласованные со спектральным составом исходного сигнала.
(интервал
дискретизации), согласованные со спектральным составом исходного сигнала.
Частота дискретизации, как
правило, удовлетворяет условию ![]() , где
, где ![]() – верхняя граничная частота в спектре
исходного сигнала (функции)
– верхняя граничная частота в спектре
исходного сигнала (функции) ![]() , из которой формируется
кусочно-постоянная функция
, из которой формируется
кусочно-постоянная функция ![]() . Если система
. Если система
временных интервалов ![]() задана, то каждая функция
задана, то каждая функция ![]() полностью определяется вектором
полностью определяется вектором 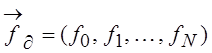 из
из ![]() . Базисной
системе
. Базисной
системе 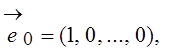
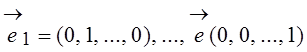 соответствует система
прямоугольных функций, которая для
соответствует система
прямоугольных функций, которая для ![]() приведена на рис. 6.13.
приведена на рис. 6.13.
Очевидно, что это
ортогональная система функций, так как для любой пары функций 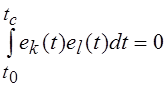 при
при ![]() .
.
Для того чтобы эта
система была ортонормальна, необходимо, чтобы амплитуды импульсов были бы равны
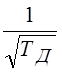 . Совокупность базисных функций можно
задать с помощью матрицы, которая для нашей базисной системы имеет вид
. Совокупность базисных функций можно
задать с помощью матрицы, которая для нашей базисной системы имеет вид 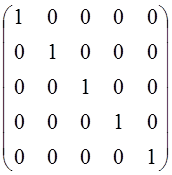 , т. е. является единичной матрицей
, т. е. является единичной матрицей ![]() .
.
Система функций Хаара.
В 1900 г. венгерский
математик Альфред Хаар предложил и исследовал ортонормальную систему функций на
промежутке ![]() , к которому с помощью операции
масштабирования и сдвига может быть преобразован любой конечный отрезок. Схема
построения функций Хаара была рассмотрена в гл.4.
, к которому с помощью операции
масштабирования и сдвига может быть преобразован любой конечный отрезок. Схема
построения функций Хаара была рассмотрена в гл.4.
Являясь полной
ортонормальной системой в ![]() , система функций Хаара
обладает замечательным свойством: для любой непрерывной на
, система функций Хаара
обладает замечательным свойством: для любой непрерывной на
промежутке ![]() функции
функции ![]() ряд
Фурье–Хаара
ряд
Фурье–Хаара 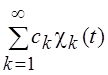 , где
, где 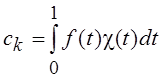 , сходится равномерно:
, сходится равномерно:
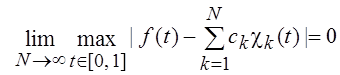 .
.
Однако ряды Фурье–Хаара сходятся довольно медленно, причем темп сходимости, в отличие от тригонометрического базиса, не зависит от гладкости (непрерывности и наличия непрерывных производных) представляемой функции.
При фиксированном
разбиении основного промежутка на двоичные отрезки (фиксировано m)
функции Хаара, отвечающие данному m, образуют базис на множестве
кусочно-постоянных функций, которые можно построить на данной системе отрезков.
При ![]() система функций Хаара превращается в базис
система функций Хаара превращается в базис ![]() . Это замечание в полной мере относится и к
системе функций Уолша, о которой мы поговорим несколько позже.
. Это замечание в полной мере относится и к
системе функций Уолша, о которой мы поговорим несколько позже.
Для иллюстрации рассмотрим представление в базисе Хаара треугольного импульса вида
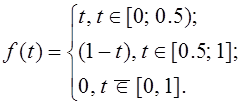
Учитывая вид ![]() , можно утверждать, что модуль
коэффициентов ряда Фурье–Хаара
будет зависеть только от m, причем коэффициенты стоящие перед функциями
Хаара, располагающимися на промежутке
, можно утверждать, что модуль
коэффициентов ряда Фурье–Хаара
будет зависеть только от m, причем коэффициенты стоящие перед функциями
Хаара, располагающимися на промежутке ![]() будут
отрицательными, а на промежутке
будут
отрицательными, а на промежутке ![]() – положительными.
– положительными.
Таким
образом, 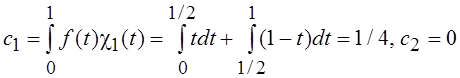 , так как по отношению к середине
промежутка
, так как по отношению к середине
промежутка ![]() – четная функция, а
– четная функция, а ![]() – нечетная. Коэффициенты
– нечетная. Коэффициенты ![]() для левой половины отрезка
для левой половины отрезка ![]() будут равны:
будут равны:
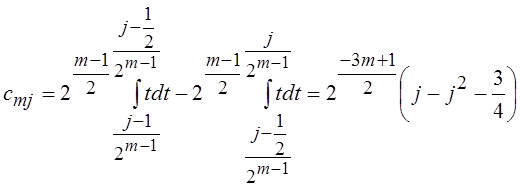 ,
, ![]() .
.
Для правой половины – 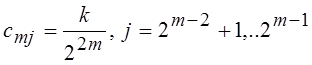 .
.
На рис. 6.14, а
приведена исходная функция ![]() и результат ее аппроксимации
первыми членами ряда Фурье–Хаара.
и результат ее аппроксимации
первыми членами ряда Фурье–Хаара.
Для сравнения на рис.
6.14, б приведен результат аппроксимации ![]() в
тригонометрическом базисе с тем же числом членов.
в
тригонометрическом базисе с тем же числом членов.
Отметим, что для
тригонометрического базиса скорость сходимости ряда Фурье зависит от гладкости
раскладываемой в ряд функции. Так, если ![]() непрерывна
вместе с
непрерывна
вместе с ![]() первыми производными, то коэффициенты ряда
Фурье убывают по закону
первыми производными, то коэффициенты ряда
Фурье убывают по закону 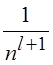 , где
, где ![]() – номер коэффициента ряда Фурье,
– номер коэффициента ряда Фурье, ![]() соответствует непрерывности функции.
соответствует непрерывности функции.
Таким образом, для
рассматриваемой функции коэффициенты Фурье в тригонометрическом базисе убывают
по закону ![]() . Для базиса Хаара темп сходимости не
зависит от степени гладкости функции и имеет порядок
. Для базиса Хаара темп сходимости не
зависит от степени гладкости функции и имеет порядок 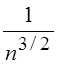 .
.
Суммируя по ![]() функции Хаара, соответствующие одному и
тому же
функции Хаара, соответствующие одному и
тому же ![]() и умножая результат суммирования на
и умножая результат суммирования на 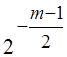 , приходим к функциям Радемахера
, приходим к функциям Радемахера 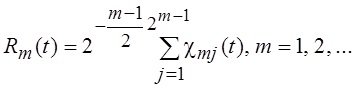 .
.
Другая форма определения функций Радемахера
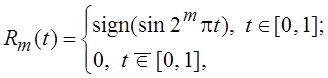
часто бывает более наглядной.
Функции Радемахера
образуют на промежутке ![]() ортонормальную систему, т. е.
ортонормальную систему, т. е. 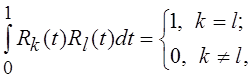 , но она не полна, т.к. содержит лишь
нечетные по отношению к середине промежутка, функции.
, но она не полна, т.к. содержит лишь
нечетные по отношению к середине промежутка, функции.
На ее основе может быть
построена полная в ![]() ортонормальная система функций
Уолша, к знакомству с которыми мы и переходим.
ортонормальная система функций
Уолша, к знакомству с которыми мы и переходим.
В заключение приведем
матричное представление первых восьми функций Хаара (матрица ![]() ) и первых четырех функций Радемахера
(матрица
) и первых четырех функций Радемахера
(матрица ![]() ):
):
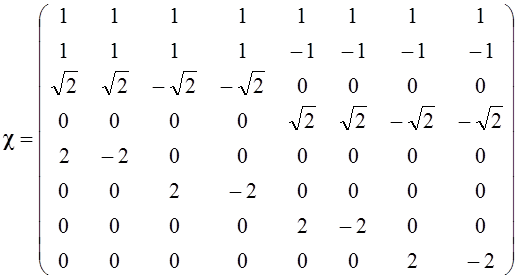 ;
; 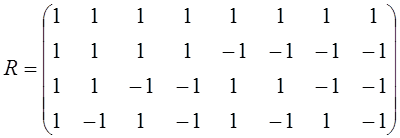 .
.
Функции Уолша
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.