Первое знакомство с
функциями Радемахера и Уолша состоялось в конце гл.4, где речь шла о построении
ортогональных систем. Там были введены функции Уолша, упорядоченные по Пэли,
при этом функция Уолша, обозначаемая при этом как ![]() , где
, где ![]() – номер функции, определялась как
произведение функции Радемахера с номерами
– номер функции, определялась как
произведение функции Радемахера с номерами ![]() . Целые
числа
. Целые
числа ![]() есть показатели степени двоичного
представления номера функции Уолша
есть показатели степени двоичного
представления номера функции Уолша ![]() ,
, ![]() . Таким образом,
. Таким образом, 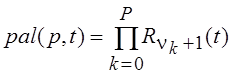 .
Ниже представлены выражения для первых восьми функций Уолша:
.
Ниже представлены выражения для первых восьми функций Уолша:
 ;
; ![]() , поскольку
, поскольку ![]() ;
;
![]() ,
поскольку
,
поскольку ![]() ;
;
![]() , поскольку
, поскольку ![]() ;
;
![]() , поскольку
, поскольку ![]() ;
;
![]() , поскольку
, поскольку![]() ;
;
![]() , поскольку
, поскольку ![]() ;
;
![]() ,
поскольку
,
поскольку![]() .
.
Матрица, определяющая
первые восемь функций Уолша (m = 3), упорядоченных по Пэли, и
обозначаемая обычно как ![]() имеет вид
имеет вид
 .
.
Часто более удобным
оказывается способ упорядочивания функции Уолша по Адамару, суть которого
состоит в следующем. Введем в рассмотрение прямое произведение матрицы ![]() и матрицы
и матрицы ![]() , обозначаемое как
, обозначаемое как ![]() и
определяемое как блочная матрица вида
и
определяемое как блочная матрица вида
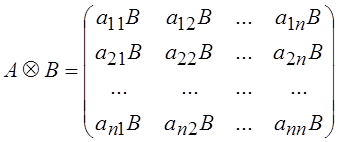 .
.
Например,
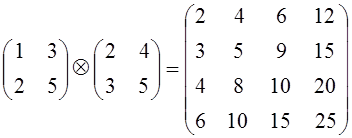 .
.
Запишем матрицу 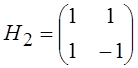 и с помощью операции прямого произведения
получим матрицы
и с помощью операции прямого произведения
получим матрицы
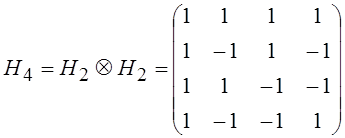 ,
,
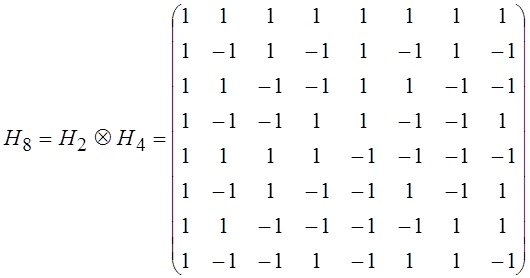
и т. д. Матрицы ![]() , получаемые по этой схеме, называются матрицами
Адамара. Их строки определяют функции Уолша, упорядоченные по Адамару и
обозначаемые как
, получаемые по этой схеме, называются матрицами
Адамара. Их строки определяют функции Уолша, упорядоченные по Адамару и
обозначаемые как ![]() , где
, где ![]() – номер
функции,
– номер
функции, ![]() .
.
Третий из используемых на
практике способов упорядочивания функций Уолша называется упорядочивание по
секвенте (числу перемен знака или нулей функции Уолша на рассматриваемом
интервале). Он очень близок к тому, который был предложен Уолшем, следствием
чего является используемое обозначение ![]() .
Функции, упорядоченные по секвенте могут быть определены с помощью матрицы
.
Функции, упорядоченные по секвенте могут быть определены с помощью матрицы ![]() . Так, матрица
. Так, матрица ![]() имеет
вид:
имеет
вид:
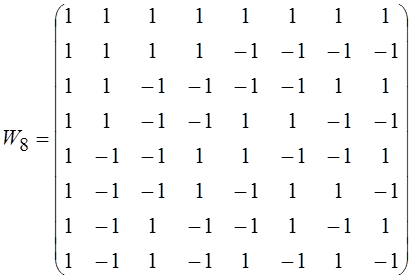 .
.
Между номерами функций при различных способах упорядочивания существует взаимно однозначное соответствие. Матрицы, с помощью которых задаются функции Уолша, обладают рядом особенностей, определяющих свойства функций Уолша.
1.
Это ортогональные
матрицы (скалярные произведения любых двух строк равно нулю). Матрица ![]() называется ортогональной, если
называется ортогональной, если ![]() , где
, где ![]() –
скаляр. В нашем случае
–
скаляр. В нашем случае ![]() .
.
2.
Замена ![]() -ой строки на
-ой строки на ![]() -ый
столбец не меняет матрицу. Это означает, что если вместо непрерывного времени
-ый
столбец не меняет матрицу. Это означает, что если вместо непрерывного времени ![]() рассматривать дискретное – номера двоичных
отрезков, то переменные
рассматривать дискретное – номера двоичных
отрезков, то переменные ![]() и
и ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() являются равноправными.
являются равноправными.
3. Сумма элементов каждой строки, кроме первой, равна нулю. Это свойство определяет уравновешенность функции Уолша.
4.
Поэлементное
произведение любых двух строк дает строку этой матрицы с номером ![]() (
(![]() ), где
), где ![]() и
и ![]() –
номера перемножаемых строк, а записанная операция означает суммирование по
модулю 2. Это свойство определяет мультипликативность системы функций Уолша.
–
номера перемножаемых строк, а записанная операция означает суммирование по
модулю 2. Это свойство определяет мультипликативность системы функций Уолша.
Система функций ![]() называется мультипликативной, если произведение
любых двух функций системы дает функцию системы и для любой функции
называется мультипликативной, если произведение
любых двух функций системы дает функцию системы и для любой функции ![]() , функция
, функция ![]() также
входит в систему.
также
входит в систему.
Хорошо знакомым примером
мультипликативной системы является система комплексных экспонент ![]() .
.
Остановимся теперь на
вопросах представления функций в базисе (базисах) Уолша. Как уже неоднократно
отмечалось, система функций Уолша полна в ![]() . Это
означает, что для
. Это
означает, что для ![]() выполняется соотношение:
выполняется соотношение:
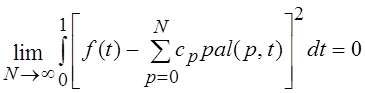 .
.
Аналогичные утверждения справедливы и
для ![]() и
и ![]() .
.
Для равномерной
сходимости рядов Фурье–Уолша необходимо, чтобы функция ![]() была
непрерывна и имела на интервале
была
непрерывна и имела на интервале ![]() ограниченное полное
изменение (ограниченную вариацию). Функция
ограниченное полное
изменение (ограниченную вариацию). Функция ![]() имеет
на промежутке
имеет
на промежутке ![]() ограниченную вариацию, если при
любом разбиении промежутка
ограниченную вариацию, если при
любом разбиении промежутка ![]() , и при любом
, и при любом ![]() совокупность сумм вида
совокупность сумм вида  , отвечающая всевозможным разбиениям промежутка
, отвечающая всевозможным разбиениям промежутка
![]() , ограничена.
, ограничена.
Точную верхнюю грань 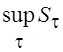 называют полной вариацией функции
называют полной вариацией функции ![]() на
на ![]() и
обозначают как
и
обозначают как 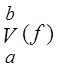 .
.
Из самой идеи построения
функций Уолша видно, что для получения конечной совокупности функций Уолша
необходимо задать m определяющее число двоичных отрезков, на которых
задаются значения функций Уолша. Построенная система будет полна на множестве
кусочно-постоянных функций, построенной на данной системе отрезков, но не будет
полна в ![]() .
.
Пусть представляемая
кусочно-постоянная функция ![]() определена своими
значениями
определена своими
значениями ![]() на заданных двоичных отрезках, т. е. задан
вектор
на заданных двоичных отрезках, т. е. задан
вектор ![]() . Тогда выражение для коэффициента
Фурье-Уолша (для определенности будем использовать упорядочивание по Адамару)
примет вид
. Тогда выражение для коэффициента
Фурье-Уолша (для определенности будем использовать упорядочивание по Адамару)
примет вид
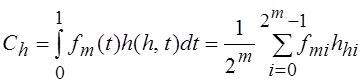 ,
,
где ![]() – i-й
элемент h-ой строки матрицы
– i-й
элемент h-ой строки матрицы ![]() .
.
Таким образом,
коэффициент Фурье с точностью до постоянного при данном m множителя ![]() определяется скалярным произведением
вектора значений кусочно-постоянной функции
определяется скалярным произведением
вектора значений кусочно-постоянной функции ![]() и
вектора, определяющего соответствующую функцию Уолша.
и
вектора, определяющего соответствующую функцию Уолша.
Вся совокупность
коэффициентов ряда Фурье–Уолша, определяемая вектором ![]() ,
кусочно-постоянной функции
,
кусочно-постоянной функции ![]() может быть найдена как
произведение матрицы Уолша (
может быть найдена как
произведение матрицы Уолша (![]() ) на вектор
) на вектор ![]() , т. е.
, т. е. 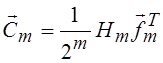 , где
символ «T» означает транспонирование.
, где
символ «T» означает транспонирование.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.