Другие предметы \ Математический аппарат радиотехники

Ортогональные системы кусочно-постоянных функций, страница 3

Так как элементы матриц  равны , то для вычисления спектра требуется  операций сложения или вычитания. Это число можно уменьшить до  за счет структурных особенностей матриц Уолша. Поясним это на примере, взяв, как и прежде m = 3.

Для вектора  компоненты вектора , определяющего спектр Уолша в системе Адамара, будут равны (общий множитель 1/8 опущен):

;

;

;

;

;

;

;

.

Как уже отмечалось, требуемое число сложений и вычитаний равно . Экономия в вычислениях достигается за счет группирования слагаемых, входящих в исходное выражение. Вычислим восемь чисел по правилу: ; ; ; ; , ; ; . После этого выражения для коэффициентов  примут вид:

; ; ;

; ; ;

; .

Вычислим еще восемь чисел: ; ;; ; ; ; ; . После этого вычисляются коэффициенты :

; ; ; ; ;

; ; .

На это уйдет еще восемь операций. Общее число операций, как и было указано выше, будет  вместо исходных 56. С ростом m выигрыш в числе операций нарастает. Число операций уменьшается в 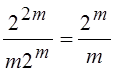  раз. Приведенная процедура определяет “быстрое” преобразование Адамара–Уолша.

Формализация “быстрого” преобразования состоит в факторизации матрицы преобразования, т.е. представлении ее в виде произведения матриц такого же порядка, содержащих большое количество нулей.

Так, для нашего примера матрица Адамара–Уолша  записывается как произведение трех (m = 3) одинаковых матриц вида

.

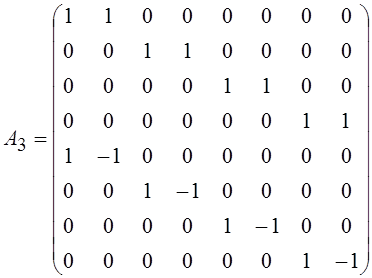Записывая процедуру умножения матриц на вектор, исключающую умножение на 0, мы получаем алгоритм “быстрого” преобразования, который мы рассмотрели выше.

Контрольные вопросы

1.  Дайте определение комплексного числа. Приведите алгебраическую и показательную форму представления комплексного числа.

2.  Сформулируйте правила сложения, умножения, возведения в степень и извлечения корня из комплексного числа.

3.  Дайте определение непрерывности функции комплексного переменного.

4.  Запишите условия дифференцируемости функции f(z) = u(x, y) + jv(x, y).

5.  Дайте определение аналитической функции, аналитичной в области D. Приведите примеры.

6.  Как определяется интеград от функции комплексной переменной?

7.  Сформулируйте теорему Коши об интеграле по замкнутому контуру.

8.  Что такое ряд Лорана для функции f(z)? Что называется главной частью ряда Лорана?

9.  Что такое вычет функции f(z) в точке z = a? Как он вычисляется?

10.  Как с помощью вычетов можно вычислить интеграл вида 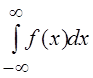? Приведите примеры.

11.  Дайте определение аналитического продолжения функции f(z).

12.  Дайте определение гамма-функции. Приведите основное функциональное соотношение для гамма-функции.

13.  Как получается асимптотическое представление гамма-функции Г(х) при x >> 1? В чем сущность метода Лапласа?

14.  Как определяется бета-функция? Как она связана с гамма-функцией? Какое применение находят гамма- и бета-функции в теории вероятностей? Что такое неполная гамма- и бета-функция?

15.  Дайте определение интеграла вероятностей Ф(х) и укажите его связь с другими формами представления erf x,erfc x.

16.  Дайте определение интегралов Френеля и укажите их асимптотические свойства.

17.  Дайте определение ортогональных многочленов и сформулируйте их основные свойства.

18.  Сформулируйте признак, по которому выделяются классические ортогональные многочлены.

19.  Дайте определение полиномов Лежандра, Чебышева (1-го и 2-го рода), Якоби, Лагерра и Эрмита.

20.  Какие функции называются цилиндрическими? Какова их классификация?

21.  Приведите основные функциональные соотношения для функций Jv(x) и Iv(x).  Охарактеризуйте особенности их применения.

22.  Приведите пример использования свойств функций Бесселя в задаче отыскания спектра сигнала s(t) = Umcos(w0t + bsinWt), где Um – амплитуда сигнала, b = Dw/W – индекс модуляции, Dw – девиация частоты, W – частота модулирующего гармонического колебания.

23.  Какие функции относятся к функциям гипергеометрического типа?

24.  Как определяется гипергеометрический ряд? Какие ограничения накладываются на его параметры?

25.  Какие функции называются кусочно-постоянными?

26.  Дайте определение системы функций Хаара. Приведите первые восемь функций этой системы.

27.  Найдите первые четыре члена ряда Фурье–Хаара для функции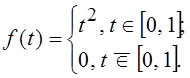

28.  Дайте определение системы функций Радемахера. Почему они не могут быть базисной системой?

29.  Дайте определение функций Уолша при различных сопособах упорядочивания.

30.  Что такое быстрое преобразование Уолша и в чем его алгоритм?

Скачать файл