Для винеровского СП, с
которым мы познакомились раньше, ![]() =0,
=0, ![]() =
=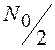 , и уравнение (8.1)
примет вид
, и уравнение (8.1)
примет вид
![]()
![]() =
=![]()
![]()
![]() , (8.2)
, (8.2)
где 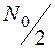 - СПМ
нормального белого шума, интегрированием которого получается винеровский
процесс. Если при
- СПМ
нормального белого шума, интегрированием которого получается винеровский
процесс. Если при ![]() =0
=0 ![]() =
=![]() , т.е.
, т.е. ![]() =
=![]() , то решением уравнения (8.2) для
бесконечного пространства (отсутствие границ) будет
, то решением уравнения (8.2) для
бесконечного пространства (отсутствие границ) будет 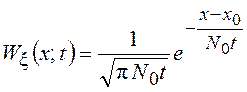 .
.
Контрольные вопросы
1. Дайте определение марковского процесса.
2. Как определяется простая цепь Маркова?
3. Что такое переходная вероятность?
4. Как определяется
матрица перехода за ![]() шагов?
шагов?
5. Что такое финальные вероятности?
6. При каких условиях гауссовский процесс будет также Марковским?
7. Какому уравнению удовлетворяет ПВ диффузионного марковского процесса?
8. Как выглядит уравнение Колмогорова-Чепмена для винеровского процесса? Каким будет его решение?
Глава 9. Прямые способы описания случайных процессов
В рассмотренной выше классификации случайных процессов в основу были положены способы описания, опирающиеся на многомерные распределения значений процесса в различные моменты времени, или их предельную форму – функционалы ПВ. Однако, для многих приложений более продуктивным является способ описания, основанный на непосредственной функциональной связи значений процесса в данный момент времени с его предыдущими значениями, находящимися под действием случайных возмущений. Эта связь может задаваться в виде рекуррентных алгоритмов, разностными, дифференциальными, интегральными уравнениями или их комбинациями и называется прямым способом описания случайного процесса.
Примером прямого описания СП является его моделирование с помощью электронно-вычислительной машины (ЭВМ) с использованием датчиков случайных чисел.
Важным примером такого
подхода являются случайные процессы, полученные на основе регрессионной модели,
называемой также параметрической моделью случайного процесса. Это представление
можно интерпретировать, как выход цифрового фильтра, находящегося под действием
возбуждающей случайной последовательности, т.е. 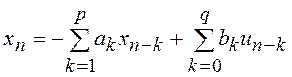 , где
, где ![]() - элементы формируемой случайной
последовательности, числа
- элементы формируемой случайной
последовательности, числа ![]() и
и ![]() являются параметрами модели,
являются параметрами модели, ![]() - входная возбуждающая случайная последовательность,
в роли которой обычно выступает дискретный нормальный белый шум (
- входная возбуждающая случайная последовательность,
в роли которой обычно выступает дискретный нормальный белый шум (![]() - независимые нормальные случайные
величины с нулевым средним значением и дисперсией
- независимые нормальные случайные
величины с нулевым средним значением и дисперсией ![]() ).
).
Если возмущающая
последовательность ![]() является дискретным белым шумом,
то модель называется авторегрессионной – скользящего среднего (АРСС). Числа
является дискретным белым шумом,
то модель называется авторегрессионной – скользящего среднего (АРСС). Числа ![]() и
и ![]() определяют
порядок модели.
определяют
порядок модели.
Структурная схема
формирования случайной последовательности (временного ряда) на основе АРСС
приведена на рис. 36. Как это принято, ![]() -
элемент задержки последовательности на один такт.
-
элемент задержки последовательности на один такт.
Частными случаями
АРСС-модели являются модель скользящего среднего (СС), для которой все коэффициенты
![]() равны нулю, и авторегрессионная (АР)
модель, у которой, наоборот, все коэффициенты
равны нулю, и авторегрессионная (АР)
модель, у которой, наоборот, все коэффициенты ![]() , кроме
, кроме ![]() , равны нулю. Структурные схемы
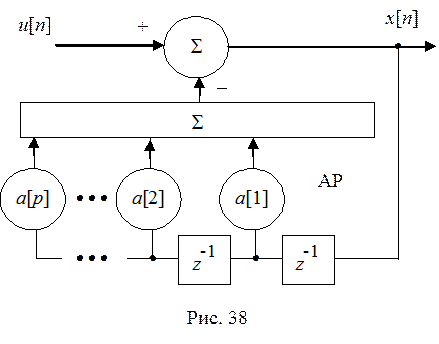
формирователей последовательностей СС и АР приведены на рис. 37, 38 соответственно.
, равны нулю. Структурные схемы
формирователей последовательностей СС и АР приведены на рис. 37, 38 соответственно.
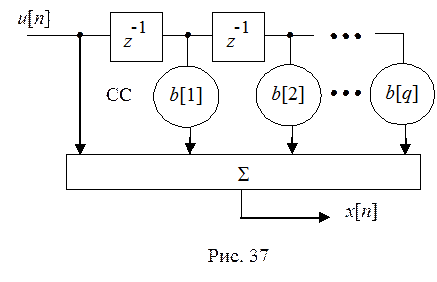 Рассмотренные модели
формирования случайных последовательностей связаны друг с другом. Так,
например, АРСС и СС модели можно записать с помощью АР модели в общем случае
бесконечного порядка. Это позволяет использовать большое число эффективных моделей
оценивания параметров АР модели с последующим вычислением параметров другой
модели. С подробностями можно познакомиться с помощью [14, с. 221].
Рассмотренные модели
формирования случайных последовательностей связаны друг с другом. Так,
например, АРСС и СС модели можно записать с помощью АР модели в общем случае
бесконечного порядка. Это позволяет использовать большое число эффективных моделей
оценивания параметров АР модели с последующим вычислением параметров другой
модели. С подробностями можно познакомиться с помощью [14, с. 221].
Одно из важных применений параметрического описания СП состоит в решении задачи оценивания АКФ или СПМ процесса, заданного дискретными отсчетами (случайной последовательности, временного ряда).
 Суть метода состоит в
подборе порядка модели и её параметров таким образом, чтобы оцениваемая
последовательность и последовательность формируемая моделью были бы максимально
близки в определенном смысле.
Суть метода состоит в
подборе порядка модели и её параметров таким образом, чтобы оцениваемая
последовательность и последовательность формируемая моделью были бы максимально
близки в определенном смысле.
После этого в качестве оценки АКФ или СПМ исходной последовательности используются АКФ или СПМ последовательности, формируемой моделью. Более подробно эти вопросы будут рассмотрены в разделе, посвященном методам оценки характеристик случайных процессов. Здесь же рассмотрим в качестве примера простейшую АР модель первого порядка
![]() .
.
Можно показать, см. например
[15, стр. 575], что для такой последовательности коэффициент корреляции ![]() имеет вид
имеет вид ![]() , где
введено обозначение
, где
введено обозначение ![]()
Для СПМ с помощью Z преобразования будем иметь 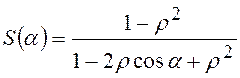 , где a – безразмерный аргумент СПМ,
, где a – безразмерный аргумент СПМ, ![]() , где
, где ![]() - интервал дискретизации (период, с
которым следуют элементы последовательности
- интервал дискретизации (период, с
которым следуют элементы последовательности ![]() ). Периодический
характер СПМ определяется дискретностью
). Периодический
характер СПМ определяется дискретностью ![]() . Дисперсия
в установившемся режиме будет равна
. Дисперсия
в установившемся режиме будет равна 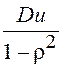 , где
, где ![]() – дисперсия дискретного нормального белого
шума
– дисперсия дискретного нормального белого
шума ![]() . Вид зависимости
. Вид зависимости ![]() от
k, при
от
k, при ![]() ,
называемой коррелограммом, и спектр приведены на рис. 39.
,
называемой коррелограммом, и спектр приведены на рис. 39.
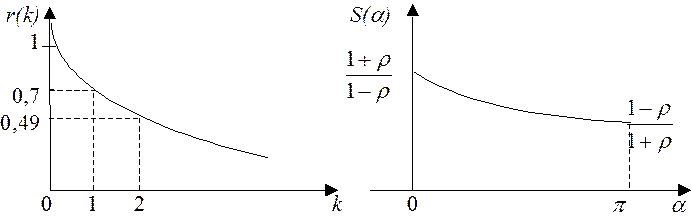
Рис. 39
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.