Прямые способы описания случайных процессов, страница 2

Отметим, что если возмущающая последовательность  является последовательностью независимых гауссовских СВ с нулевыми средними и дисперсиями , то регрессионная последовательность будет гауссовско – марковской.

Случайные процессы, задаваемые стохастическими дифференциальными или интегральными уравнениями

Рассмотрим дифференциальное уравнение

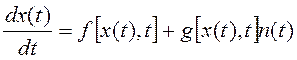                                (9.1)

с начальным условием , где f и g – детерминированные функции, удовлетворяющие условию Липшица, т.е. для

,

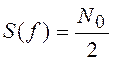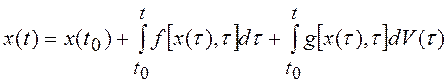, n(t) – нормальный белый шум с нулевым средним значением и . Уравнения, в которые входят белые шумы, или при эквивалентных формах записи  и , где 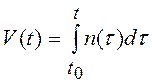– винеровский процесс и  называют стохастическими дифференциальными уравнениями (от греческого слова «стохастос» – случай) процесса.

Входящие в эти уравнения выражения типа 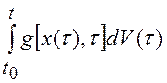, а также интегралы вида 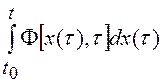,  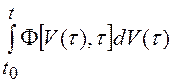называются стохастическими интегралами, если F – непрерывно дифференцируемая функция своих аргументов, х(t) – диффузионный марковский процесс с коэффициентами сноса A₁(x,t) и диффузии A₂ (x,t), непрерывными по обоим аргументам. Строгая математическая теория стохастических интегралов была создана японским математиком К. Ито и развита отечественным ученым Р.Л. Стратоновичем. Не останавливаясь на математических деталях определения стохастических интегралов [5], сформулируем теорему Дуба [16], определяющую класс систем первого порядка, выходные процессы которых являются марковскими дифференциальными процессами.

Случайный процесс x(t), заданный стохастическим уравнением (9.1) является марковским.

При этом коэффициенты сноса и диффузии в прямом уравнении Колмогорова или уравнении Фокера – Планка (8.1) определяются как  и 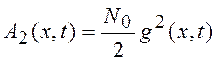, где обозначено x=x(t). При этом стохастические дифференциальные уравнения (9.1) понимаются в смысле Ито [15].

При описании стохастической динамики реальных систем, на вход которых действуют достаточно гладкие (дифференцируемые) случайные процессы, замена входного процесса нормальным белым шумом с соответствующим значением СПМ 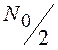, будет корректной при использовании симметризированной формы стохастического дифференциального уравнения (по Стратоновичу).

Применительно к уравнению (10.1) это даст следующие выражения для коэффициентов сноса 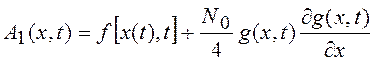 и диффузии .

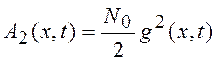Как видно, различие в интерпретации стохастического интеграла (в смысле Ито или смысле Стратоновича) сказывается лишь на значении коэффициента сноса. Если коэффициенты сноса и диффузии не зависят от времени, то стационарная ПВ может быть найдена как решение обыкновенного дифференциального уравнения первого порядка.

Рассмотрим примеры.

1. Винеровский процесс.

Для винеровского процесса уравнение (10.1) имеет вид

,

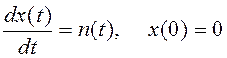где n(t) – нормальный белый шум.

Коэффициенты диффузии и сноса равны соответственно  и 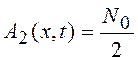, а уравнение Фокера – Планка имеет вид

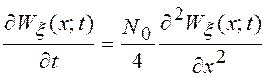
Его решением, как уже отмечалось выше, будет

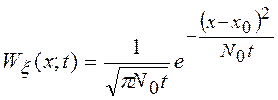
2. Интегрирующая RC цепь под действием нормального «белого» шума.

Дифференциальное уравнение для данной цепи имеет вид

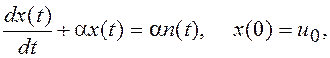
где  – постоянная времени цепи. Это линейное неоднородное уравнение имеет решение .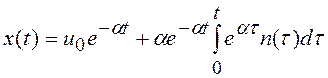

Заметим, что как линейное преобразование гауссовского процесса n(t), x(t) будет также гауссовским процессом.

Его математическое ожидание , так как .

Аналогично нетрудно показать (сделать самим), что дисперсия 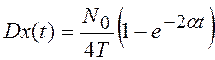, а корреляционная функция 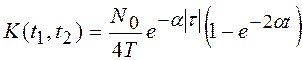, где  – СПМ нормального белого шума, а , .

Как видно из приведенных выражений процесс становится становится стационарным лишь в установившемся режиме, при .

Уравнение Фокера – Планка для данного процесса имеет вид

.

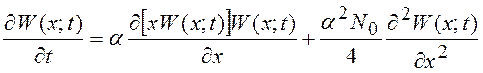Его решением будет нормальное распределение вида

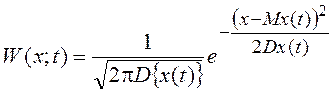
 На рис. 41 представлена динамика изменения  с течением времени.

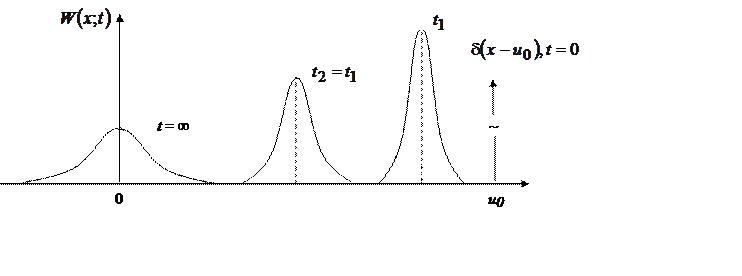
Рис. 40

В рассмотренных примерах стохастическое уравнение, формирующее процесс, было линейным и в силу этого сформированный процесс являлся гауссово-марковским.

Если уравнение (10.1) нелинейно, то процесс, оставаясь марковским, гауссовским уже не будет.

Например, если стохастическое уравнение имеет вид [17],

,

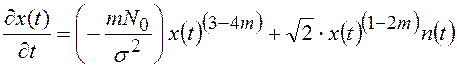где , , то стационарное распределение будет являться распределением Накагами

,

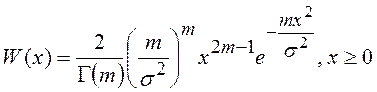которые часто используются для описания амплитудных флуктуаций сигнала после прохождения турбулентной среды.

При m=1 распределение Накагами переходит в релеевское с параметром .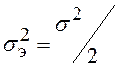

Контрольные вопросы

1. Что из себя представляют прямые способы описания СП?

2. Что называется регрессионной или параметрической моделью СП?

3. Рассмотрите модель авторегрессии – скользящего среднего (АРСС) и ее частные случаи.

4. Опишите свойства процессов, задаваемых стохастическими дифференциальными уравнениями.

5. Как выглядит стохастическое уравнение для винеровского процесса?

6. Проанализируйте с позиций стохастических уравнений действие нормального «белого» шума на интегрирующую RC-цепь.