Оптимизация динамики национального дохода

10.2. Оптимизация динамики национального дохода

Критерии и условия оптимизации. Конечные цели развития социалистической экономики в наибольшей степени отражает динамика потребления c(t). Поэтому для оптимизации динамики национального дохода за фиксируемый плановый период [0, T] в качестве максимизируемой целевой функции естественно взять

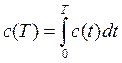
т.е. максимизировать суммарный фонд потребления за плановый период[1].

Более общий подход к максимизации потребления за период учитывает, что эффект от единицы потребления (потребительский эффект) в разные моменты времени неравнозначен и может быть измерен посредством некоторой функции q = q(t).

Функция q(t) называется взвешивающей. Она сопоставляет, или "взвешивает", потребление в разные моменты времени. Общепризнанной является гипотеза о существовании потребительских предпочтений во времени: полезный эффект благ настоящего выше полезного эффекта благ будущего. В соответствии с этой гипотезой взвешивающая функция q(t) должна обладать следующими свойствами: 1) q(t) > 0, т.е. потребление в любой момент времени увеличивает интегральный уровень потребления; 2) q(t) — монотонно убывающая функция (с убывающими "весами"); 3) , т.е. "вес" потребления отдаленного будущего стремится к нулю.

Удобно в качестве взвешивающей функции взять убывающую экспоненту q(t) =  при w> 0. В начальный момент времени потребление имеет вес q(0) = 1, а затем вес убывает с непрерывным темпом w;  Например, при w > = 0,05 имеем q(5) = 0,779, q(10) = 0,607, q(20) = 0,368 (о научных подходах к объяснению и количественной оценке предпочтений потребления во времени см. в ДМНХ, с. 60-61).

Итак, более общая целевая функция дисконтированного потребления, частным случаем которой (при w= 0) является (10.16), имеет вид

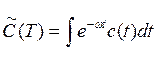               (10.17)

Возможности оптимизации динамики национального дохода, заданной уравнением

,

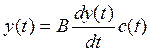заключаются в регулировании соотношения между потреблением и накоплением. Рассмотрим несколько возможных подходов.

Оптимизация с нерегулируемой нормой накопления. Анализируемые ниже оптимизационные динамические модели национального дохода включает в качестве ограничивающего условия уравнение распределения национального дохода на накопление и потребление, фигурировавшее в 10.1 как самостоятельная модель. Особенность данного условия в рамках оптимизационной модели в том, что с(t) становится эндогенной переменной.

Максимизация суммарного потребления без учета инвестиционного лага. Совмещение простейшей модели динамики национального дохода (10.5) и целевой функции (10.16) дает оптимизационную модель

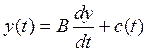                       (10.18)

.

Представим (10.18) в виде задачи оптимального уравнения с критерием

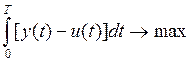
Применение принципамаксимумаПонтрягина позволяет получить аналитические решения. Они существенно различаются для краткосрочного и долгосрочного периодов планирования (при этом граница, разделяющая краткосрочный и долгосрочный периоды, определяется величиной капиталоемкости национального дохода)[2].

1. При Т£ В имеем следующую оптимальную траекторию:

u*(t)=0, y*(t) = c*(t) = y(0),

a*(t) = 0, С*(T) y(0)T

Таким образом, когда длительность планового периода не превосходит коэффициента капиталоемкости национального дохода, накопление и экономический рост вообще неэффективны. В данном случае динамический оптимум — это простое воспроизводство национального дохода и его полное использование на потребление. Величина В характеризует минимальный срок, в рамках которого накопление может быть эффективным с точки зрения "интересов" потребления (см. замечания по этому поводу в 6.4). В этом смысле динамическая модель при Т £ В сходна со статической.

Очевидно, что по крайней мере в рамках краткосрочного и среднесрочного планирования производственное накопление не может рассматриваться как полностью эндогенная переменная. Необходимо обеспечивать определенный уровень накопления исходя из интересов развития в послеплановом периоде.

2. При Т > В оптимальная траектория качественно изменяется в точке t = Т - В.

Для t Î[0, Т-В] имеем у*(t) =у(0) , u*(t) =y*(t}, c*(t)= 0, a*(t) = 1, т.е. на первом этапе планового периода весь национальный доход используется на накопление и увеличивается максимально возможным (технологическим) темпом.

Для t Î[Т-В, T]оптимальная траектория имеет вид

y*(t) = y*(T-B) = y(0), u*(t) = 0

c*(t) = y*(t), a*(t) = 0

Объем национального дохода стабилизируется и весь используется на потребление:

C(T) = By(0)exp.

Таким образом, в точке t= Т — В происходит так называемое релейное переключение режима воспроизводства национального дохода, что является необходимым условием достижения максимума C(T). Заметим, что первое релейное переключение происходит в точке t= 0: скачок накопления с u(0) до y(0) и падение потребления от с(0) до нуля.

Рис 10.2. Траектории развития в задачах оптимального управления (у -национальный доход; с - потребление; и - производственное накопление:

а) без дисконтирования потребления; б) с дисконтированием потребления.

Оптимальные траектории развития при Т > В изображены на рис. 10.2a. Национальный доход — кривая KLM, накопление - KLNP, потребление — ONLM. Площадь заштрихованного прямоугольника NLMPравна С*(Т).

При В = 3,5 и Т = 10 максимальный уровень национального дохода (3846) достигается в t= 6,5; С*(10) = 13452. При Т = 20 точка переключения сдвигается на 10 лет (t= 16,5), благодаря чему достигается фантастический рост национального дохода и суммарного потребления. Для сравнения укажем, что при росте с постоянной нормой накопления a= 0,20 и тех же прочих исходных данных суммарный фонд потребления за 10 лет составляет 6474, а за 20 лет — 17 940.