Основная модель межотраслевого баланса

6.2. Основная модель межотраслевого баланса

Одним из важнейших теоретических принципов моделирования народного хозяйства является совместный анализ материально-вещественных и стоимостных взаимосвязей (принцип двойственности). Общие выводы, вытекающие из такого подхода к процессу общественного воспроизводства, рассматривались в гл. 3. Основные соотношения межотраслевого баланса общественного продукта (6.2) и (6.4) позволяют более конкретно анализировать совместно два аспекта межотраслевых связей: а) по производству и распределению продукции; б) по формированию общественных издержек производства и цен.

Модель межотраслевых материально-вещественных связей. Соотношения I и II квадрантов межотраслевого баланса общественного продукта (6.2) характеризуют зависимости между (2n + n²) величинами х_i, у_ix_ij. Но они носят слишком общий характер. Для построения математической модели решающее значение имеет предположение о том, что x_ijесть функция от объема производства этой продукции: . Подставим значения x_ij в (6.2), получим систему из п уравнений:

            (6.9)

В простейшей модели используется предположение о пропорциональной зависимости между затратами и объемами производства, т.е. вводятся линейные однородные функции производственных затрат:

(6.10)

Коэффициент пропорциональности  называют коэффициентом прямых затрат продукции iна производство единицы продукции j. Эти коэффициенты в совокупности образуют квадратную матрицу

A = (a_ij), i, jÎI.

В табл. 6.2 приводятся коэффициенты прямых материальных затрат, полученные в результате обработки ряда межотраслевых балансов СССР[1].

Таблица 6.2

Коэффициенты прямых материальных затрат межотраслевого баланса СССР

*   Включает все отрасли промышленности, кроме легкой и пищевой

** Включает собственно легкую промышленность, а также пищевую

Подставив значения a_ijиз (6.10) и (6.9), получаем систему из п линейных алгебраических уравнений с 2n переменными х_i и y_i.

(6.11)

Или

где δ_ij — элемент единичной матрицы:

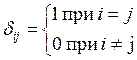
В векторно-матричной форме имеем

X=AX+Yили (E—A)X=Y,(6.13)

где X = (x_i) — вектор-столбец объемов производства; Y = (у_i) — вектор-столбец конечной продукции; Е — единичная матрица порядка п.

Данная система может иметь единственное решение, если из общего количества переменных величин х_iи у_jчисло неизвестных не превышает числа уравнений (это условие является необходимым, но недостаточным). Принятие одних величин за известные, а других — за неизвестные определяется постановкой конкретной экономической задачи (см. 6.6).

Систему уравнений (6.13) можно представить в виде

X=(E-A)^-1Y(6.14)

где (E-A)^-1— матрица, обратная к (Е — А). Вопрос о существовании и свойствах такой матрицы рассматривается в 6.3.

Таблица 6.3

Коэффициенты матрицы (Е - А) межотраслевого баланса СССР