Оптимизация динамики национального дохода, страница 5

Выход на режим роста с постоянной нормой накопления. Каждая из рассмотренных выше задач оптимизации динамики национального дохода "в чистом виде" обладает определенными недостатками. Очевидно, что с помощью только формальных методов оптимизации соотношения потребления и накопления вряд ли можно добиться приемлемых результатов. Проведенный анализ позволяет сформулировать ряд требований к динамике национального дохода и его структуры:

1)  норма накопления не должна неограниченно приближаться к 0 и 1;

2)  должны быть сглажены релейные переключения и накопления;

3)  получаемое решение (в том числе с постоянной оптимальной нормой накопления) в начале периода не должно сильно зависеть от выбираемой его длительности.

Эти требования можно выполнить, сочетая рассмотренные выше постановки задач (как с заданием траекторий с(t),так и с максимизацией потребления) на различных интервалах долгосрочного планового периода в соответствии с поставленными целями.

Рассмотрим задачу постепенного выхода на режим роста с постоянной нормой накопления.

Начальная норма накопления составляет а(0). В течение планового периода [0, T] необходимо выйти наиболее высокую норму  и в дальнейшем поддерживать ее постоянной.

Переходный режим развития определяется на отрезке [0, ] , так что.

Постепенное увеличение a(t) может быть обеспечено, в частности, при постоянном темпе прироста потребления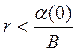.Тогда в соответствии с (10.9) при норма накопления будет монотонно увеличиваться от а₀ до а.

                                   а)б)

Рис. 10.6. Динамика нормы накопления: постепенное увеличение до фиксированной постоянной (а) и постоянной оптимальной (б).

Момент достижения заданной нормы накопления определяется из уравнения , которое имеет единственное решение (см. рис. 10.6а). Это — точка пересечения возрастающей кривой а(t) и ординаты a(t) = . Увеличивая r, можно увеличивать tи наоборот. Например, требуется перейти от исходной нормы накопления а(0) = 0,17 к  = 0,20. При r= 0,03 получаем  = 1,64, при r = 0,04 получаем = 2,96.

Постоянная норма накопления может не задаваться, а определяться одновременно с переходом на режим развития с оптимальной нормой накопления в зависимости от продолжительности оставшегося планового периода. Тогда  и  определяются из уравнения a() = а*( Т —), которое также имеет единственное решение (см. рис. 10.6б). Это точка пересечения возрастающей кривой a(t) и убывающей кривой а*(T—), рассчитанной путем оптимизации постоянной нормы накопления. Пусть, к примеру, r = 0,03, Т — 20. В этом случае пересечение двух кривых происходит = 0,9 и a() =a*(T—) = 0,5.

Изложенный подход применим и в том случае, когда начальную норму накопления целесообразно уменьшить: . Тогда следует выбрать 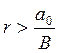. Это обеспечивает постепенное снижение a{t) до  за промежуток [0, ] , где  <Т.

Рассмотренные макромодели выявляют качественные свойства оптимальных траекторий национального дохода при различных способах экономического регулирования. Каждая модель в отдельности обладает определенными недостатками, которые, как правило, являются гипертрофированными достоинствами (предельное использование той или иной возможности получения лучшего решения с точки зрения формального критерия). Теоретическая и практическая ценность моделей данного типа существенно возрастает при их комплексном применении.