Оптимизация динамики национального дохода, страница 2

Каков же реальный смысл оптимума задачи (10.18)? По-видимому, получаемое решение можно трактовать как технологически достижимый оптимум (с точки зрения максимума интегрального потребления), который не может быть превзойден при заданном параметре В. И с этой точки зрения задача (10.18) близка модели (10.5) при с(t) = 0, в которой определяется технологический темп прироста национального дохода. Безусловно, такой оптимум не удовлетворяет многим требованиям социально-экономического характера, т.е. априори не является социально-экономическим оптимумом. Но надо отдавать отчет в том, что включение в модель дополнительных условий (в частности, сглаживание релейного режима) неизбежно уменьшает величину технологически достижимого интегрального фонда потребления.

Главными недостатками решения задачи (10.18) являются его сильная зависимость от величины Т и релейное изменение структуры национального дохода. Очевидно, что экономически недопустимы участки развития как с полным отсутствием потребления, так и простого воспроизводства с отсутствием накопления. Неприемлемым является также резкое изменение траектории развития в зависимости от величины Т: при ее уменьшении (так, что Т £ В) становится неэффективным накопление, при значительном же увеличении (или использовании принципа скользящего планирования) момент потребления вообще не наступает. Важный теоретический результат анализа модели — выявление особой роли коэффициента В в процессе воспроизводства.

Максимизация дисконтированного потребления без учета инвестиционного лага. Можно предположить, что релейный характер динамики национального дохода в оптимизационной модели обусловливается недостатком применяемой целевой функции, в которой равные объемы потребления в разные моменты времени учитываются как равноценные. Поэтому целесообразно проанализировать модель с целевой функцией (10.17) вместо (10.16):

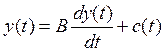  ,           (10.19)

Важную роль в анализе модели (10.19) играет величина "скорректированной капиталоемкости".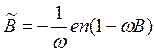

Функция  — возрастающая при .

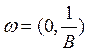При малом  коэффициент мало отличается от В: . Например, (0,05) =3,85, (0,10) = 4,31. Поведение решения (10.19) существенно зависит также от того, соблюдается ли условие wB <. 1. Поскольку общепринятые оценки параметра w находятся в интервале 0,05 - 0,10, данное неравенство выполняется с большим запасом; это обстоятельство используется в последующем анализе.

Анализ модели (10.19) с использованием принципа Понтрягина приводит к выводу, что качественный характер ее оптимальной траектории не изменяется по сравнению с решением модели (10.18).

1. При Т £ национальный доход не растет и весь используется на потребление. Поскольку > В, то длительность периода, в рамках которого накопление неэффективно, увеличивается по сравнению с задачей на максимум недисконтированного суммарного потребления.

2. При Т> оптимальная траектория имеет релейное переключение в точке t= Т —. Рост с максимальным темпом 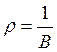заканчивается раньше, чем в модели (10.18). Максимальный уровень национального дохода

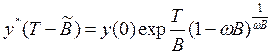
меньше, чем в точке переключения модели (10.18). Хотя "этап потребления" становится более продолжительным, суммарный фонд потребления С* = y* (T—) оказывается меньше из-за более низкого постоянного уровня потребления.

На рис. 10.2б изображены траектории развития, соответствующие максимуму дисконтированного потребления, и их смещения по сравнению с рис. 10.2а. Площадь N’L’М’Р меньше площади NLMP.

При w = 0,05 и Т = 10 максимальный уровень национального дохода (3480) достигается в t=6,15; С*(10) = 13398. При w — 0,10 максимум национального дохода достигается раньше (вt= 5,69), но его объем уменьшается (3051). Снижается и суммарный объем потребления (13150) -

Итак, надежда на то, что благодаря дисконтированию можно устранить релейный характер динамики национального дохода и сильную зависимость оптимальной траектории от величины Т, не оправдалась. Необходимы более радикальные способы регулирования динамики и структуры национального дохода.