Оптимизация динамики национального дохода, страница 3

Оптимизация с учетом инвестиционного лага. Отметим основные особенности оптимального решения задачи, включающей сосредоточенный инвестиционный лаг  ( в соответствии с (10.12)).

Первая особенность выражается в том, что при t Î [0, ] динамика национального дохода предопределяется динамикой накопления в предплановом периоде: y(t) = y₀(t). На этом участке можно управлять только распределением национального дохода. Оптимальное решение имеет вид и* (t) =0, с*(t) = y₀(t). Принцип максимума применяется при Т >.

Если < Т £  + В, то по-прежнему накопление неэффективно и весь национальный доход должен направляться на потребление. Максимальное значение у(t) достигается в точке.

Инвестиционный лаг увеличивает длительность планового периода, в рамках которого накопление неэффективно с точки зрения интересов потребления.

Развитие с релейным переключением осуществляется при Т> + В. Здесь в отличие от оптимальных решений (10.18) - (10.19) выделяются четыре (а не два) участка развития:

а) при tÎ[0, ] динамика объема национального дохода предопределена: у* (t) —у_о(t), весь национальный доход направляется на накопление;

б) при t Î [, Т -  - В] национальный доход растет максимально возможным темпом и по-прежнему весь используется на накопление;

в) при tÎ [Т —— В, Т - В]национальный доход продолжает расти, но уже весь направляется на потребление;

г) при tÎ [Т - В, Т] объем национального дохода остается неизменным и весь используется на потребление.

Таким образом, при Т>  + В основные качественные характеристики оптимальных траекторий сохраняются и с учетом инвестиционного лага. Но при этом момент релейного переключения смещается к началу планового периода и появляются два участка инерционного роста дохода tÎ [0, ] иtÎ [Т -  - В, Т - В], равных по продолжительности величине лага (см. рис. 10.3).

Оптимизация с динамическими и структурными ограничениями. Рассмотрим два подхода к улучшению свойств оптимальных траекторий. Оба они связаны с включением дополнительных условий, ограничивающих резкие скачки темпов и структуры национального дохода.

Включение условия непрерывного роста потребления. Простейший способ получения гладкой траектории потребления — замена интегральной целевой функции С(Т) условием максимизации параметра непрерывного роста потребления:

c(t) = c(0)exp(rt) (10.20)

Анализ решения данной задачи обнаруживает качественное сходство с решением уравнения (10.9) при r> р₀. Накопление непрерывно уменьшается и в точке t₁становится равным нулю. Одновременно нулевым становится и темп прироста национального дохода. Следовательно, максимизация потребления осуществляется в ущерб будущему экономическому развитию (подробнее см. ДМНХ, с. 68).

Рассмотрим более гибкое условие непрерывного роста потребления. Для этого разделим объем потребления на две части: экзогенную (растущую с минимально необходимым темпом r< р₀) и эндогенную (оптимизируемую):

c(t) = c₁(t)+c₂(t),

c₁ (t) = c (0)exp(rt),       (10.21)

Рис. 10.3. Рост национального дохода в задаче оптимального управления с инвестиционным лагом.

Применение принципа максимума Понтрягина дает следующие результаты:

1.  При Т<В получаем такое же решение, как и для задачи (10.18). Это вполне объяснимо, поскольку условие роста c_l (t) перекрывается ростом с₂ (t). По-прежнему накопление в рамках периода продолжительностью Т<В неэффективно.

2.  При Т>В оптимальная траектория, как и для моделей (10.18) - (10.19), имеет ряд характерных участков с границей t = Т — В.

На первом участке темп прироста национального дохода непрерывно увеличивается, на накопление выделяется максимально допустимая часть национального дохода, потребление растет минимально необходимым темпом г. На втором участке объем национального дохода остается неизменным и весь используется на потребление (см. рис. 10.4).

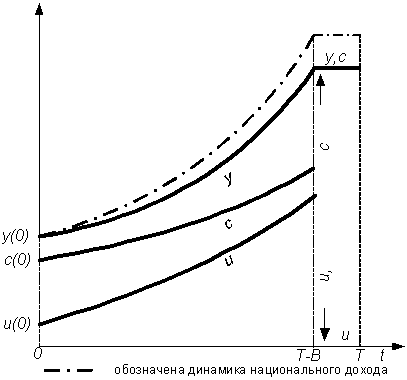
Рис. 10.4. Траектория развития в задаче оптимального управления с минимальным ростом потребления.