Модели расширяющейся экономики и магистральное развитие

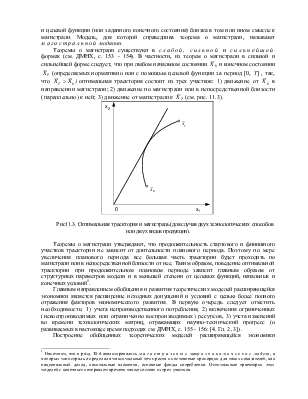
11.2. Модели расширяющейся экономики и магистральное развитие

Основные понятия. В рамках экономической статики изучались понятия допустимых и эффективных технологий, технологических множеств, а также важнейшие их свойства (см. гл. 4). Здесь мы будем рассматривать обобщения этих понятий для дискретного времени t= 0, 1, ..., Т (Т £ ¥). Отрезок времени между соседними моментами [t, t + 1] называется элементарнымотрезкомвремени.

Пусть X(t) — n-мерный вектор затрат в момент t, Y(t+ 1) — n-мерный вектор выпуска продукции в момент t+ 1. Технологическая допустимость пары (X, Y) означает возможность, используя технологию периода t, получить в момент t + 1 из затрачиваемых в момент tингредиентов вектора Xвектор продукции Y. Совокупность всевозможных допустимых технологий (X, Y) в момент tобразует технологическое множество Z_t. В теоретических моделях экономической динамики используется ряд предположений о структуре технологического множества, на основе которых доказываются основные теоремы о свойствах эффективных технологий и технологического множества (см. ДМНХ, с. 145 - 148).

Технологически возможная траектория представляет собой последовательность {(X_t, Y_t+ 1) Î Z_t, t = 0,1 Т- 1}. Такая траектория допустима, если вектор Х_о совпадает с заданным начальным состоянием Х_о. Укажем на два типа таких траекторий.

Первый тип траекторий характеризуется тем, что Y_t+1 = X_t+1, т.е. продукты воспроизводятся в замкнутой производственной системе без каких-либо "входов" и "выходов". Тогда технологически допустимая траектория составляет последовательность {X_t}, t =0,…, Т, такую, что (X_t, X_{t + 1}) Î Z_t.

Траектория называется эффективной (по конечному состоянию), если для всякой допустимой траектории {X_t}из соотношения  следует, что .

Рассматриваемый тип траекторий используется при изучении предельных возможностей роста. Непроизводственное потребление в этом случае можно учитывать в векторах X_tкак дополнительные нормативные затраты.

Второй тип траекторий учитывает потребление в явном виде. Производимая продукция разделяется на две части — производственное и непроизводственное потребление: Y_t= X_t+ C_t. Для такого типа траекторий понятие эффективности трансформируется. Выделение эффективных траекторий из допустимых осуществляется только путем сравнения векторов потребления.

Траектория , Î Zt, t = 0, …, Т - 1 называется эффективной, если для всякой траектории Î Zt, t = 0, ..., T - 1 из соотношений следует, что  t= 1, …, T.

Важной характеристикой существующего множества Zявляется технологический темп роста, определяемый следующим образом.

С каждым технологическим процессом (X, Y) ÎZсвязывают число 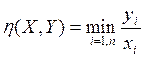, являющееся темпом роста данного процесса.  Технологическим темпом роста называется число

При естественных предположениях относительно Zтехнологическому темпу роста  соответствует траектория

, t = 1, …, T

Она называется траекторией максимального сбалансированного роста, или магистралью.

Впервые существование магистрали в структурных моделях экономической динамики обнаружил Дж. фон Нейман. Поэтому магистраль (траектория максимального сбалансированного роста) именуется неймановской траекторией или неймановским лучом.

Посредством теоретических моделей рассматриваемого типа изучается не только технологический, но и ценностный аспект экономики. Вводится понятие цен, устанавливающих взаимное соответствие между эффективными (оптимальными) технологиями и рентабельностью (в том числе максимумом прибыли; см. ДМНХ, с. 146 — 148).

Модель Неймана. Первой и наиболее известной абстрактной моделью расширяющейся экономики является модель Дж. фон Неймана, сформулированная еще в начале 30-х годов.

Модель Неймана задается парой матриц А и В. Матрица А = (a_ij) характеризует затраты продуктов i = 1, ..., т при использовании различных технологических способов j =1, ..., п с единичной интенсивностью. Матрица В = (b_ij) объединяет коэффициенты выпуска соответствующих продуктов при использовании различных технологических способов с единичной интенсивностью. Обе матрицы имеют одинаковую размерность тхп. Предполагается, что числа a_ijи b_ij удовлетворяют следующим ограничениям:

(1) 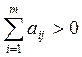 (j = 1, …, n)

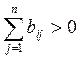(2)   (i = 1, …, m)

Условие (1) означает, что в каждом способе используется хотя бы один продукт. Условие (2) означает, что каждый продукт может быть произведен хотя бы одним технологическим способом.

Обозначим через Z= (Zj) вектор интенсивностей использования технологических способов. Тогда технологическое множество модели Неймана можно представить в следующем виде:

, Y=BZ, Z>0}.