10.5. Моделирование динамики двух подразделений общественного производства
Схемы воспроизводства К.Маркса - В.И.Ленина и макромоделирование. Схемы простого и расширенного воспроизводства, разработанные К.Марксом применительно к капиталистическому хозяйству и развитые впоследствии В.И.Лениным, играют исключительно важную роль в экономической теории социализма и методологии макромоделирования. Подробный анализ схем воспроизводства классиков марксизма-ленинизма содержится в литературе по политической экономии и общеэкономическим проблемам. Поэтому ограничимся кратким рассмотрением схем воспроизводства с точки зрения возможностей конструирования на их основе моделей экономической динамики.
Будем использовать следующие обозначения: х - объем произведенной и реализуемой продукции, с — фонд возмещения используемых средств производства, v— необходимый продукт, m— прибавочный продукт. Элементы продукции и затрат первого и второго подразделений отмечаются индексами I и II. Из анализа схем воспроизводства следует, что без поддержания определенных материально-вещественных и стоимостных пропорций невозможно ни простое, ни расширенное воспроизводство.
Балансы продукции I и II подразделений по стоимостному составу имеют вид
![]()
![]() (10.61)
(10.61)
Основное условие расширенного воспроизводства выражается неравенством
![]() (10.62)
(10.62)
Прибавочный
продукт в каждом подразделении распределяется на накопление (в средствах производства Dс и в предметах
потребления Dy) и потребление (тп) : mI = DсI+DvI +![]() , mII= DсII+ DvII +
, mII= DсII+ DvII + ![]() . При этом необходимо, чтобы величина DvI+
. При этом необходимо, чтобы величина DvI+![]() в форме средств производства была обменена на
эквивалентную величину предметов потребления, а величина DсII — в форме предметов
потребления — на эквивалентную величину средств производства.
в форме средств производства была обменена на
эквивалентную величину предметов потребления, а величина DсII — в форме предметов
потребления — на эквивалентную величину средств производства.
При расширенном воспроизводстве (с учетом накопления) в каждом годовом цикле необходимо осуществить обмен между двумя подразделениями и внутри них в следующих пропорциях (см. рис. 10.10).
|
|
Рис 10.10
Результатом обмена продукции в соответствии с рис 10.10 являются балансы распределения продукции двух подразделений:
|
|
Совмещение (10.61) и (10.63) дает систему уравнений межотраслевого баланса общественного продукта в разрезе двух подразделений.
Соотношения расширенного воспроизводства (10.61), (10.63) содержат избыточное число переменных. Поэтому для построения операционной модели (числовой или формализованной) необходимо вводить ряд дополнительных допущений о зависимостях между переменными, как правило, в виде структурных параметров.
Возможность включения в схемы воспроизводства различного рода структурных параметров и их комбинаций приводит к большому разнообразию макроэкономических моделей, конструируемых на базе схем воспроизводства. Характерным признаком этих моделей является то, что включаемые в них структурные параметры относятся как к материально-вещественным пропорциям (например, коэффициенты
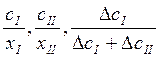
и т.п.), так и к пропорциям стоимостным (нормы прибавочного продукта в подразделениях, доли распределения прибавочного продукта подразделений на потребление, накопление средств производства, накопление предметов потребления и т.п.)[1].
Динамика двух подразделений в моделях воспроизводства общественного продукта. Проанализируем рассматривавшиеся в 10.1, 10.2, 10.4 модели воспроизводства общественного продукта и национального дохода с точки зрения динамики I и II подразделений. Возможность такого анализа облегчается тем, что в указанных моделях нами выделялись такие элементы валового общественного продукта, как фонд возмещения потребленных средств производства, фонд производственного накопления, фонд непроизводственного потребления и накопления, формируемые за счет производства либо средств производства, либо предметов потребления.
Линейные модели с экзогенной динамикой потребления. Объемы производства продукции I подразделения и II подразделения в соответствии с обозначениями, принятыми в 10.1, удовлетворяют равенствам:
![]() ,
, ![]() (10.64)
(10.64)
Пусть r1 и r2 - темпы прироста продукции I и II подразделений; g1 и g2 — доли I и II подразделений в валовом общественном продукте (g1 + g2 =1). Тогда
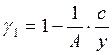 ;
; 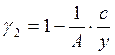 (10.65)
(10.65)
Систематизируем основные выводы, вытекающие из анализа трех типов экономического развития, различающихся темпами прироста потребления и динамикой нормы производственного накопления. Вначале будем исходить из того, что параметры макротехнологии — коэффициенты A и В — не изменяются во времени.
1.
Постоянная
норма накопления: a(t) =а0, r= 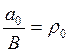 .
.
Поскольку ![]() и
и 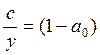 , то
, то ![]() ,
, 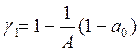 ,
, 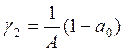 .
.
Итак, темпы двух подразделений постоянны и одинаковы; доли подразделений в валовом продукте не изменяются. Вводя прежние исходные данные (А = 2,5, В = 3,5, а0 = 0,20), получаем r0 = 0,057, g1 = 0,68, g2- 0,32.
2. Уменьшающаяся норма накопления как следствие r >r0.
Доля II подразделения растет за счет уменьшения нормы производственного накопления: r2 >r1.Однако темпы прироста валового продукта и национального дохода падают. В точке t1эти темпы становятся нулевыми; еще раньше
— при t= ![]() < t2достигает максимума и
начинает
уменьшаться продукция I подразделения. В точке t2нулевым становится
объем продукции I подразделения. Например, при r= 0,08 находим
< t2достигает максимума и
начинает
уменьшаться продукция I подразделения. В точке t2нулевым становится
объем продукции I подразделения. Например, при r= 0,08 находим ![]() =3,24, t1= 4,98,
=3,24, t1= 4,98, ![]() =9,8.
=9,8.
3. Увеличивающаяся норма накопления как следствие r<r0.
Доля I подразделения и темп I подразделения растут
за счет увеличения нормы накопления. Пределами их роста являются: 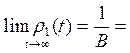 0,286,
0,286, ![]() .
Например, при r= 0,04 имеем r1(5) = 0,11, r1.(10) = 0,185, r1(20) = 0,275, g1(5) = 0,73, g1(10) = 0,82, g1(20) = 0,97.
.
Например, при r= 0,04 имеем r1(5) = 0,11, r1.(10) = 0,185, r1(20) = 0,275, g1(5) = 0,73, g1(10) = 0,82, g1(20) = 0,97.
Общий вывод состоит в том, что при сделанных допущениях (в частности, неизменности коэффициентов А и В) монотонно снижающаяся или монотонно повышающаяся доля I подразделения может быть оправдана только на ограниченных интервалах времени, когда ставятся задачи резкого ускорения роста уровня жизни или резкого увеличения производственного потенциала.
Рассмотрим теперь, какое влияние на динамику соотношения двух подразделений оказывает изменение во времени коэффициентов А и В.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.