Моделирование межотраслевых взаимосвязей производства, личного потребления и доходов населения

7.3. Моделирование межотраслевых взаимосвязей производства, личного потребления и доходов населения

В основной модели межотраслевого баланса связи производства, потребления и доходов населения отражаются односторонне. Модель позволяет анализировать, как потребление населения воздействует на производство (Y^{П →} X), а объемы производства влияют на формирование доходов населения (X^→ Z), но при этом допускается возможность независимых изменений объемов и структуры потребления и условий оплаты труда. Естественно стремление замкнуть контур связей производства, потребления и доходов, построить более общую модель для комплексного исследования межотраслевых зависимостей.

Рассматриваемая расширенная модель межотраслевого баланса имеет следующие особенности:

в составе продукции, направляемой для конечного использования y_i, выделяется часть, реализуемая за счет доходов населения y_i (z), и "прочая" конечная продукция

y_i = y_i(z) +                 (7.12)

где z равен той части совокупного дохода населения, которая расходуется на приобретение товаров и услуг;

в модель включается баланс доходов населения, в котором выделяются доходы, получаемые в сфере производства z_j, и "прочие" доходы:

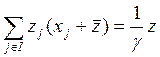,  (7.13)

где g — доля потребительских расходов в совокупном доходе населения; вводится условие баланса расходов населения:

           (7.14)

Отметим, что соотношения (7.12), (7.13) по своему экономическому содержанию соответствуют строке и столбцу "население" межотраслевого баланса денежного оборота.

Общая модель включает условия (7.12), (7.13) и систему уравнений производства и использования продукции:

, iÎI(7.15)

Основная задача плановых расчетов по модели (7.12) — (7.14) — определение объемов производства x_iи доходов населения z при заданных объемах "прочей" конечной продукции и "прочих" доходов населения.

Типовые функции покупательского спроса y_i(z)) рассматривались в 5.3. Некоторые из них носят ярко выраженный нелинейный характер. Однако кусочно-линейная аппроксимация функций потребления позволяет сохранить линейность общей модели межотраслевых связей и приемы ее структурного анализа. Линейная аппроксимация функций потребления дает тем лучшие результаты, чем в меньших интервалах изменяется доход. Именно такая ситуация имеет место при использовании расширенной модели в краткосрочном прогнозировании и планировании. Это дает возможность с успехом применять линейные функции при ожидаемых интервалах изменения дохода . Линейные функции потребления обладают еще тем преимуществом, что избавляют от необходимости включать в общую межотраслевую модель условие (7.13). Если все показатели межотраслевого баланса даются в ценностном выражении, то равенство выполняется автоматически при построении линейных уравнений регрессии способом наименьших квадратов (в этом случае ; .

В условиях действующей системы оплаты труда величина дохода, получаемого в каждой отрасли производства, также ^может быть представлена в виде линейной функции  — коэффициент пропорциональности оплаты труда и объема производства,  - величина дохода, не зависящая от объема производства.

Введем векторно-матричные обозначения в расширенной модели:

 , ,

Получаем следующую систему уравнений межотраслевых зависимостей производства, потребления и доходов:

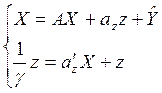(7.16)

Система (7.15) обладает свойствами, во многом аналогичными свойствам основной модели межотраслевого баланса. Матрицу этой системы

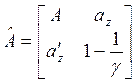
можно называть продуктивной, если существует такой неотрицательный вектор [XZ]¢ ≥0, что

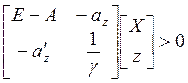
Будем исходить из того, что в системе (7.16) продукция измерена в ценах и матрица А удовлетворяет достаточным условиям продуктивности неразложимых матриц модели межотраслевого баланса (т.е.  для всех jÎIи хотя бы для одного j).

Для того чтобы матрица  была продуктивна, должны выполняться условия, более жесткие по сравнению с условиями продуктивности матрицы А, так как система межотраслевых связей получает дополнительную нагрузку в виде затрат на личное потребление и "затрат" дохода[1].

Необходимым и достаточным условием продуктивности является полуположительность матрицы

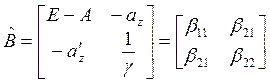
Основное свойство анализируемой расширенной модели межотраслевого баланса состоит в том_, что при продуктивности матрицы любому положительному векторусоответствует единственный полуположительный вектор .