Моделирование межотраслевых взаимосвязей производства, личного потребления и доходов населения, страница 2

Рассмотрим особенности элементов матрицы , являющихся коэффициентами полных затрат в межотраслевой системе, охватывающей взаимосвязи производственного потребления, оплаты труда, структуры личного потребления. В соответствии с формулами обращения блочных матриц имеем:

β₁₁= (E - A)^-1+(E - A)^-1a_za¢_z(E - A)^-1R

β₁₂= (E - A)^-1a_z R

β₂₁= R¹a¢_z(E - A)^-1

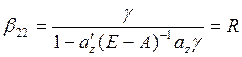
В образовании всех коэффициентов полных затрат принимает участие множитель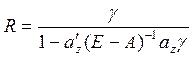

Он определяет знаки всех элементов обратной матрицы и их порядковые соотношения с коэффициентами полных затрат основной модели межотраслевого баланса.

Коэффициент β₂₂ =Rхарактеризует прирост расходной части доходов населения на единицу прироста фиксированного дохода 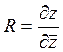.Очевидно, что для полуположительности всех элементов матрицы необходимо и достаточно, чтобы R > 0. Если же R> 1, то все ненулевые коэффициенты матрицы  превышают соответствующие коэффициенты полных затрат основной модели межотраслевого баланса.

Величина Rзависит от двух коэффициентов: а'_z (Е – A) ^-1a_zи g. Покажем, что в нормальных экономических условиях а'_z (Е – A) ^-1a_z≤ 1.

Исходим из того, что

, jÎI

т. е. сумма материальных затрат и оплаты труда не выше цены в каждой отрасли. В векторно-матричной форме это выражается как е (Е - А) > а¢_г, где е = (1, 1,..., 1). Умножим обе части неравенства на (Е - A) ^-1 a_z. Получим е (Е — А) • (Е —A) ^-1 a_z≥ a'_z (E– A) ^-1 a_z, откуда ea_z≥ a¢_z (E– А) ^-1  • a_z. Но так как ea_z= 1, то a¢_z (Е - A) ^-1 a_z ≤ 1, что и требовалось доказать.

Обозначим

a¢_z(Е - A) ^-1a_z= c

Тогда

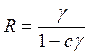
По данным усредненного межотраслевого баланса СССР за первую половину 80-х гг., с = 0,465. Значения gв экономике с относительно сбалансированным спросом и предложением колеблются вокруг единицы. Поскольку же с существенно меньше единицы, то R> 1. Действительно, при указанном с условие R> 1 выполняется при g> 0,683, т.е. при расходовании населением ежегодно более 68,3 % получаемых доходов. В частности, при g=1 получаем R = 1,869, при g= 0,8 имеем R = 1,274.

Перейдем к анализу других блоков матрицы В.

Коэффициенты блока β₁₁ характеризуют полные потребности в продукции отраслей для получения "прочей" конечной продукции. Эти коэффициенты в дополнение к коэффициентам матрицы (Е — А)^-1 включают затраты, возникающие вследствие взаимодействия производства, потребления: доходов. Сопоставления элементов матриц А, В, β₁₁показывают, что многие коэффициенты затрат расширенной модели превышают в десятки раз соответствующие коэффициенты полных и прямых затрат основной модели межотраслевого баланса. При этом в наибольшей степени возрастают затраты отраслей, формирующих основную часть фонда личного потребления.

Коэффициенты блока β₁₂ показывают полные затраты отраслей на прирост доходов, не зависящих от объемов производства. Вектор β₁₂может быть представлен в виде трех векторов: прямых затрат продукции на единицу дохода a_z , затрат, обусловленных взаимосвязями по производственному потреблению [(Е - А) ^-1 – E] a_z, и затрат, обусловленных взаимосвязями с доходами населения [(Е — A) ^-1 a_z (R —1)].

Коэффициенты вектора β₁₂ обычно в несколько раз превышают соответствующие коэффициенты вектора a_z.

Коэффициенты блока β₂₁ показывают полные затраты дохода на "прочую" конечную продукцию. Они включают: прямые доходы a'_z, доходы, обусловленные производственными связями a'_z[(Е - А)^-1  - Е] (т.е. косвенные затраты оплаты труда основной модели межотраслевого баланса), и "вторичный эффект дохода" (R —1)a'_z (Е - A)^-1. Коэффициенты полных затрат дохода (оплаты труда) расширенной модели больше соответствующих коэффициентов полных затрат основной модели в Rраз. Эти коэффициенты позволяют проследить влияние изменения объемов и структуры "прочей" конечной продукции на изменение доходов населения (примеры коэффициентов матрицы в сопоставлении с коэффициентами основной модели межотраслевого баланса приводятся в ММСЭ. С. 304 - 306).

Таким образом, включение в общую модель функций потребления и доходов населения значительно усиливает возможности анализа и планирования межотраслевых связей. Дальнейшим шагом в развитии модели межотраслевого баланса может стать введение функций потребления и доходов по группам населения, дифференцированных по уровню дохода и структуре потребительских расходов.