Моделирование сферы потребления. Целевая функция потребления

ГЛАВА 5

МОДЕЛИРОВАНИЕ СФЕРЫ ПОТРЕБЛЕНИЯ

В разделе I был сформулирован ряд важнейших проблем моделирования народного благосостояния в общей концепции планирования и управления народным хозяйством: обоснование и построение критериев, обеспечивающих выбор наилучших вариантов удовлетворения потребностей общества, соизмерение общественной полезности потребительских благ и общественных затрат на производство продукции, создание экономического механизма распределения потребительских благ. В данной главе эти проблемы рассматриваются более подробно, но в основном с точки зрения целей, задач и возможностей моделирования на народнохозяйственном уровне.

Более полное и дифференцированное исследование сферы потребления осуществляется посредством особых функциональных подсистем моделей (см. [3], [5]). Эти подсистемы включаются в многоаспектные и многофункциональные системы моделей народного хозяйства, логика построения которых рассматривается в разделе III.

5.1. Целевая функция потребления.

Соизмеримость и взаимозаменяемость потребительских благ. Целевая функция потребления (ЦФП) и = u(Y) — одна из наиболее общих математических моделей целеустремлений в сфере потребления. Она определяется на более узком множестве благ по сравнению с целевой функцией общественного благосостояния. Вектор переменных Y≥ 0 включает разнообразные виды продукции и услуг, используемых в сфере потребления, но в этот перечень не входит ряд социальных, экологических и других условий жизни общества. Такое ограничение области определения целевой функции позволяет, однако, более тщательно исследовать проблемы роста материального благосостояния.

Общие свойства ЦФП. Являясь частным случаем ЦФБ, функция u(Y) сохраняет ее общие свойства как инструмента упорядочения различных наборов (вариантов) потребительских благ с точки зрения удовлетворения потребностей общества (см. 2.2). Ряд свойств ЦФП удобно изучать, используя геометрическую интерпретацию уравнений и (Y) = с, где с — меняющийся параметр, характеризующий значение (уровень) ЦФП.

В пространстве п потребительских благ уравнению u(Y) = с соответствует определенная поверхность равноценных (или безразличных) наборов благ. В теории потребления такие поверхности получили название поверхностей безразличия[1]. На множестве допустимых значений Yможно построить семейство (карту) поверхностей безразличия. При этом важно отметить, что, хотя ЦФП определяется неоднозначно, семейство поверхностей безразличия единственно, т.е. не зависит от выбора монотонно возрастающего преобразования.

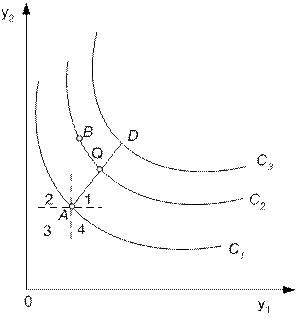Рис. 5.1. Кривые безразличия в потреблении

Рассмотрим пространство двух благ (см. рис. 5.1). Такая геометрическая интерпретация возможна, если разнообразные блага агрегировать в две группы (например, продукты питания и непродовольственные товары, включая услуги) либо рассматривать различные комбинации двух благ (потребительских комплексов) при фиксированных значениях всех других благ. Уровни ЦФП изображаются на плоскости в виде кривых безразличия. На рис. 5.1 приведены три кривые безразличия, соответствующие значениям ЦФП с₁, с₂, с₃.

Разумно для начала допустить, что функция u(Y) является строго возрастающей по всем своим аргументам, т.е. увеличение потребления любого блага при сохранении уровней