13.3. Модели с обратной рекурсией
Характерной особенностью структуры динамических моделей с обратной рекурсией является выделение двух блоков условий: а) блока расчетов на последний год планового периода; б) блока развертки решения по годам планового периода. Ниже приводятся три модели такого типа, разработанные в ГВЦ Госплана СССР, ИЭиОПП СО АН СССР и НИЭИ при Госплане СССР.
Балансовая модель с обратной рекурсией. Рассматриваемая модель предложена Б.М.Смеховым и Я.М.Уринсоном. Она входит в состав подсистемы АСПР "Сводный народнохозяйственный план". Модель включает 18 отраслей производства, в том числе две фондосоздающие (машиностроение и строительство)[1].
Условия для последнего года планового периода. В рассматриваемой модели условия для года T имеют две специфические особенности: 1) баланс основных фондов дается одним уравнением, т.е. без разбивки фондов по видам и назначению; 2) максимизируется степень достижения нормативов рациональных потребностей.
1. Балансы производства и распределения продукции:
X(T) = ATX(T) + bTu(T) + (YÑ - Y°) q + q (T), (13.7)
где и(Т) — объем чистых производственных капитальных вложений; q — степень достижения рациональных норм удовлетворения потребностей; bT— вектор материально-вещественной структуры капитальных вложений; Y° — вектор непроизводственного потребления базисного года; YÑ — вектор рациональных норм потребления; q{T) — вектор "прочей" конечной продукции (включая и Y°).
В целях упрощения расчетов функции потребления, зависящие от#, приняты линейными (в отличие от общего случая, рассмотренного в 12.3).
2. Баланс основных фондов:
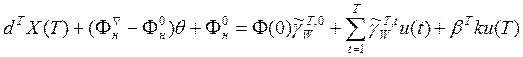 (13.8)
(13.8)
Уравнение (13.8) объединяет движение и производственных, и непроизводственных
основных фондов. Потребности в основных производственных фондах определяются как dTX(T), где dT- вектор коэффициентов
среднегодовой фондоемкости. Потребности в непроизводственных фондах (индекс
"н") определяются как сумма ![]() . Правая часть уравнения включает элементы, близкие к (12.11), в том числе дожитие фондов, вводившихся до года Т,
среднегодовой ввод фондов в году Т.
. Правая часть уравнения включает элементы, близкие к (12.11), в том числе дожитие фондов, вводившихся до года Т,
среднегодовой ввод фондов в году Т.
3. Баланс трудовых ресурсов:
lTX(T) = L(T).(13.9)
Уравнение (13.8) включает неизвестные величины u(t) не только для года Т, но и для предшествующих лет планового периода. Поэтому в модель необходимо ввести специальные условия, связывающие соответствующие эндогенные переменные для разных лет.
В рассматриваемой модели принимается
u(t) = u(0)[1+D(t)s], (13.10)
где
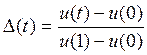 - фиксируемый коэффициент,
характеризующий отношение прироста капитальных вложений за tлет к их приросту в
первом году периода;
- фиксируемый коэффициент,
характеризующий отношение прироста капитальных вложений за tлет к их приросту в
первом году периода;
 - эндогенная переменная, означающая темп
прироста капитальных вложений в первом году периода.
- эндогенная переменная, означающая темп
прироста капитальных вложений в первом году периода.
Таким образом, условие (13.10) предопределяет закон роста капитальных вложений, но параметр этого роста не задается, а является эндогенной переменной. Если, например, принимается линейный закон роста капитальных вложений, то u(t) = u(0) + s t. В этом случае D(t) = t. Типу экономического роста с увеличивающимися абсолютными приростами соответствует ряд чисел D(t), растущих быстрее натурального ряда[2].
Подстановка (13.10) в (13.8) приводит к задаче для года Т, включающей п + 2 уравнений (13.7) —(13.9) и п + 2 неизвестных Х(Т), q, s. Решение для года Т позволяет выполнить расчеты по восстановлению всей траектории для t= 1,..., Т - 1.
Действительно, если определена величина ![]() , то по
(13.10) вычисляется траектория u(t). Затем для каждого
года tв отдельности можно находить решения системы уравнений (13.7), (13.9)
с неизвестными X(t), q.
, то по
(13.10) вычисляется траектория u(t). Затем для каждого
года tв отдельности можно находить решения системы уравнений (13.7), (13.9)
с неизвестными X(t), q.
Рассмотренная балансовая модель используется на начальных этапах разработки перспективного плана, когда еще отсутствуют детальные проектировки по отраслям. Основной функцией модели является определение сбалансированной системы показателей на последний год планового периода и оценка достижимости целевых социально-экономических показателей. Простота и компактность модели обеспечивают возможности оперативного расчета и сравнительного анализа большого числа вариантов в режиме диалога. В комплексе моделей сводного народнохозяйственного планирования результаты расчетов по данной модели используются при подготовке исходной информации и начального приближения для полностью динамической модели.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.