Модели с обратной рекурсией, страница 2

Оптимизационная модель с обратной рекурсией. Примером модели данного типа является разработанная в ИЭиОПП СО АН СССР оптимизационная межрегиональная межотраслевая модель (ОМММ). Она испо­льзуется в предплановых исследованиях территориальных пропорций народного хозяйства, в частности при подготовке региональных разделов Комплексной программы научно-технического прогресса СССР.

Статическая ОМММ рассматривается в 8.6. Ее динамизация заключается в следующем. Во-первых, капитальные вложения моделируются как воспроизводимый ресурс с оптимизируемыми параметрами роста (различными по регионам); при этом капиталовложения отражаются в балансах продукции последнего года планового периода (дополнение условий (8.39)) и в виде особых балансов капиталовложений за весь плановый период. Во-вторых, производство продукции характеризуется двумя способами: производство на мощностях, созданных до начала планового периода, и производство на мощностях, созданных в течение планового периода.

Будем рассматривать непосредственно не всю динамическую ОМММ, а ее "точечный" аналог, совпадающий также с типовым региональным блоком ОМММ (полное описание динамизированной ОМММ см. в [9, с. 267]).

1.          Балансы производства и распределения продукции года Т:

      (13.11)

Капитальные вложения учитываются по своему материально-вещественному составу U= (u_i) , i Î I,. Структура потребления задается вектором , i Î I.

2.         Ограничения по невоспроизводимым производственным ресурсам (природным, трудовым) на год Т:

,            (13.12)

где  - матрицы коэффициентов затрат ресурсов; R – вектор наличных ресурсов.

3. Балансы производственных капитальных вложений на весь плановый период:

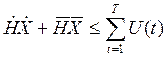,(13.13)

где — матрицы удельных капитальных затрат соответственно на поддержание производства на "старых" мощностях и для получения прироста продукции на "новых" мощностях.

4. Ограничения на объемы производства на "старых" мощностях:

,        (13.14)

где — вектор максимально возможных объемов производства, которые можно получить в последнем году планового периода на производственных мощностях, действовавших на начало планового периода.

5. Условия неотрицательности переменных:

.                  (13.15)

6.         Критерий оптимальности:

z ® max                     (13.16)

Для завершения построения модели необходимо связать друг с другом величины U(T) и 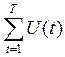. Если исходить из определенного закона роста капиталовложении в течение планового периода, то капиталовложения последнего (T -го) года и их сумма за все годы могут быть представлены в виде функций известных капиталовложений базисного года u_j(0) и неизвестных параметров ежегодного роста капиталовложений а. При линейном законе роста капиталовложений s.

u_i(T) = u_i(0) + Ts_I                              (13.17)

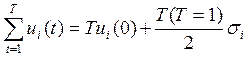,         i Î I₁   (13.18)

Подстановка этих выражений в (13.11) и (13.13) не нарушает линейности модели. Однако для развивающейся экономики более естественным является рост капиталовложений с изменяющимися абсолютными приростами.

Динамике с постоянными темпами прироста соответствуют

             (13.19)

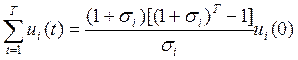, i Î I₁  (13.20)

Включение (13.19) и (13.20) в (13.11) и (13.13) дает задачу сепарабельного программирования, для которой, так же как и для задачи линейного программирования, разработаны стандартные программы численной реализации на ЭВМ, включенные в пакеты прикладных программ. Кусочно-линейная аппроксимация функций (13.19) и (13.20) приводит к задаче линейного программирования с дополнительными ограничениями. Однократное решение задачи линейного программирования дает решение исходной задачи с любой требуемой точностью (подробнее см. ДМНХ, с. 210).

Расчеты оптимальных вариантов по модели проводятся на период 10 — 20 лет. При этом наряду с определением показателей на последний год планового периода (например, 20-й) целесообразно по упрощенной модели рассчитывать (при уже известных значениях of) показатели последних лет пятилеток (т.е. 10-го, 15-го). Минимальная продолжительность расчетного периода должна быть достаточной для создания и освоения крупных мощностей.