Модели с обратной рекурсией, страница 3

Оптимизационная модель межотраслевого натурально-стоимостного баланса. Динамическая модель натурально-стоимостного межотраслевого баланса разработана в НИЭИ при Госплане СССР под руководством Ф.Н.Клоцвога. Модель предназначается для среднесрочного планирования. Отметим характерные особенности этой модели: 1) объемы капитальных вложений в целом за плановый период и в последнем году планового периода являются эндогенными переменными; 2) модель включает балансы основных производственных фондов по отраслям-потребителям; 3) критерий оптимальности — максимум объема используемого национального дохода в последнем году планового периода; 4) модель включает развернутый блок внешней торговли с эндогенными переменными объемов экспорта и импорта важнейших видов продукции; 5) учитываются условия выбора оптимальной структуры использования взаимозаменяемых материальных ресурсов (видов топлива, конструкционных материалов, сырья для легкой промышленности) в виде особых производственных способов; 6) учитываются взаимосвязи между розничным товарооборотом и всем фондом потребления; 7) вводятся ограничения на объемы производства ряда сырьевых продуктов и двусторонние ограничения по основным элементам конечного продукта.

Модель, по которой проводились расчеты к плану на одиннадцатую пятилетку, содержала около 200 основных видов промышленной и сельскохозяйственной продукции, 33 министерства и 26 отраслей народного хозяйства и промышленности. Число ограничений общего вида (не считая ограничений на отдельные переменные) — 289, число переменных — 607, что говорит о довольно широких возможностях оптимизации решений.

Поскольку большинство соотношений моделей аналогичны тем, которые включены в статическую модель натурально-стоимостного баланса и укрупненные динамические модели, рассматривавшиеся выше, ограничимся анализом двух специфических условий: а) балансов основных производственных фондов; б) условий взаимозаменяемости материальных ресурсов.

Взаимосвязи между объемами производства, капиталовложениями и основными производственными фондами во многом аналогичны (13.2) — (13.4). Специфика заключается в увязке объемов производства и капиталовложений последнего (пятого) года планового периода с капитальными вложениями и приростами основных производственных фондов за весь период (пять лет). Допускается, что капитальные вложения в течение пяти лет увеличиваются с постоянным абсолютным приростом 5 (формально он может быть и отрицательным). Тогда

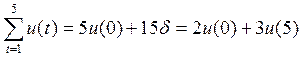
Отсюда

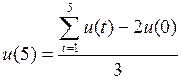         (13.21)

На основании (13.21) и следуя предположениям, используемым в (13.2) — (13.4), получаем по каждой отрасли:

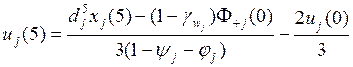                        (13.22)

где коэффициенты  в отличие от (13.4) относятся к пятилетнему периоду.

Условия взаимозаменяемости материальных ресурсов учитываются в модели следующим образом. В баланс взаимозаменяющей продукции i-го вида входит алгебраическая сумма расхода и экономии i-й продукции (r_i) в связи с взаимозаменяемостью (в дополнение к "традиционным" способам производства с коэффициентами расхода a_ij):

             (13.23)

где — объем замены продукта kпродуктом i;  — объем замены продукта iпродуктом j;  - коэффициент замены продукта i продуктом j, отражающий технологические возможности взаимозаменяемости. Значения переменных определяются в результате расчетов по модели. В частности, экспериментальные расчеты показали высокую эффективность дополнительного производства пластмасс для замены черных металлов в машиностроении и строительстве, повышении удельного веса угля в топливно-энергетическом балансе (главным образом из-за его меньшей полной металлоемкости), замены химическим волокном шерсти и хлопка. Вариантные расчеты развития народного хозяйства СССР, проведенные на основе модели, продемонстрировали ее возможности для обоснования темпов, пропорций и отраслевой структуры экономики, оценки влияния отдельных плановых решений на общеэкономические показатели, анализа воздействия различных факторов и их сочетаний на конечные народнохозяйственные результаты.