Модели расширяющейся экономики и магистральное развитие, страница 2

Наиболее характерное допущение модели Неймана состоит в том, что вся произведенная в момент tпродукция затрачивается на производство продукции в момент t+ 1:

BZ(t) ³ AZ(t+1)             (11.15)

В окончательном виде модель представляет задачу максимизации числа  — темпа роста замкнутой производственной системы:

 max,

         (11.16)

Максимальное число rj, при котором выполняется условие (11.16), называется технологическимтемпомроста и обозначается . Вектор , при котором достигается , называется оптимальным. Как уже отмечалось, этот вектор (неймановский луч) является магистралью.

По аналогии с моделью межотраслевого баланса (см. разд. 6.3) вводится понятие продуктивности. Технологическое множество модели Неймана продуктивно, если существует Z³ 0, такой, что (В — A)Z> 0. Это означает возможность превышения выпуска над затратами одновременно по всем видам продукции. Если технологическое множество продуктивно, то  > 1, следовательно, имеем расширенное воспроизводство.

Производственно-технологическим соотношениям (11.15), (11.16) можно поставить в соответствие систему ценностных соотношений. Для этого введем в рассмотрение вектор цен Р = .

Общая оценка продукции, произведенной j-м способом при его использовании с единичной интенсивностью, равна 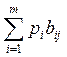, а общие затраты в ценностном выражении — 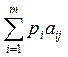.Тогда величина

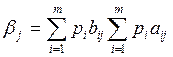
есть показатель "рентабельности" j-го технологического способа.

Задача определения ценностных соотношений формулируется следующим образом. Определить неотрицательный вектор Р и число b, для которых

b ® min         (11.17)

PB £  bPA

Величину принято называть экономическим темпом роста модели, а соответствующий этой величине вектор цен  — оптимальным. Величина означает минимальный уровень рентабельности, при котором суммарная оценка произведенной продукции не превышает суммарной оценки затрат по всем производственным способам.

Задачи (3.29) и (3.31), определяющие оптимальные структуры производства и цен, технологический и экономический темпы роста, называются двойственными. Во многом эта пара сходна с двойственными задачами математического программирования.

Отметим, что задачи (11.16) и (11.17) являются однородными, и, следовательно, оптимальные векторы  и определяются лишь с точностью до положительного множителя. Это свойство связано с замкнутостью модели и отличает (11.16) и (11.17) от двойственных задач математического программирования. Доказывается, что для рассмотренных задач всегда . Если матрицы А и В неразложимы (точнее, модель "неприводима"), то .

Взаимообусловленность материальных и ценностных свойств модели определяется системой неравенств

, Z ³ 0                 (11.18)

, P ³ 0                 (11.19)

                        (11.20)

                        (11.21)

Решение (Z, P,) системы (11.18) - (11.21), удовлетворяющее условию PBZ > 0, существует, причем p_i = 0 тогда и только тогда, когда

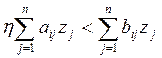
z_j = 0 тогда и только тогда, когда

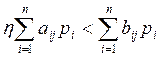
Приведенные соотношения схожи с условиями двойственной задачи линейного программирования, и им может быть дана аналогичная экономическая интерпретация: 1) для оптимальных технологических способов суммарная оценка выпуска равна суммарной оценке затрат; 2) если в технологическом способе суммарная оценка затрат превышает суммарную оценку выпуска, то такой способ неоптимален; 3) если оптимальная цена продукта положительна, то по такому продукту балансовое соотношение производства и распределения продукции реализуется как равенство; 4) если баланс производства и распределения продукции выполняется как строгое неравенство, то цена данного вида продукции равна нулю.

Частный случай модели Неймана. Пусть в каждом технологическом способе выпускается только один продукт и каждый продукт производится только одним способом. Это означает, что число продуктов равно числу способов (i, j, = 1,..., п), матрица В — единичная, матрица A — матрица межотраслевого баланса, Z= Xи означает вектор объемов производства.

Задача максимизации темпа роста производства в этом случае принимает вид

,

           (11.22)

Важным свойством данной задачи является то, что ее решение удовлетворяет условию

           (11.23)

Выпуск всех продуктов растет одинаковым темпом, и отсутствует перепроизводство каких-либо продуктов. Соотношение (11.23) можно записать в виде

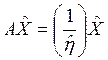              (11.24)

Легко видеть, что  — положительное собственное значение матрицы А (корень Фробениуса - Перрона), — соответствующий этому собственному значению собственный вектор. Тем самым устанавливается соответствие между математическим понятием собственно го значения матрицы и экономическим понятием максимального темпа роста производства. Необходимым и достаточным условием расширенного воспроизводства (существования  > 1) является продуктивность матрицы А.