Задача определения темпа экономического роста и сбалансированных цен в рассматриваемом случае имеет вид
![]() (11.25)
(11.25)
![]()
При
неразложимой матрице А имеем ![]() , а оптимальные векторы
, а оптимальные векторы ![]() и
и ![]() строго
положительны и единственны (с точностью до положительного множителя).
строго
положительны и единственны (с точностью до положительного множителя).
Пример 11.4.
Применим частный случай модели Неймана для анализа двухотраслевой системы. Возьмем матрицы материальных затрат (A) капитальных затрат (B) из примера 3.1. Предположим, что основные производственные фонды служат 8 лет; тогда при равномерном росте производства и фондов ежегодно должна возмещаться 1/8 капитальных затрат. Добавив 1/8 коэффициентов капиталоемкости к матрицей, получим
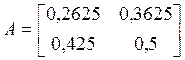
Максимальное
собственное число матрицы А равно 0,79, откуда ![]() =1,266.
Полагая
=1,266.
Полагая ![]() = 1, получаем
= 1, получаем ![]() = 1,459. Видим, что оптимальное
соотношение объемов производства довольно
близко к соотношению на магистральной траектории замкнутой системы В.Леонтьева
(пример 3.1).
= 1,459. Видим, что оптимальное
соотношение объемов производства довольно
близко к соотношению на магистральной траектории замкнутой системы В.Леонтьева
(пример 3.1).
При
переходе к формуле экспоненциального роста ![]() = 1,266)
получаем непрерывный темп прироста
= 1,266)
получаем непрерывный темп прироста ![]() = 0,236. Эта
величина достаточно близка к технологическим
темпам прироста, рассчитанным в 10.1 и 11.1 по макроэкономической и межотраслевой
моделям воспроизводства.
= 0,236. Эта
величина достаточно близка к технологическим
темпам прироста, рассчитанным в 10.1 и 11.1 по макроэкономической и межотраслевой
моделям воспроизводства.
Использование
результатов теоретического анализа. Важнейший результат анализа моделей расширяющейся
экономики состоит в доказательстве существования магистрали — траектории
максимального пропорционального роста (т.е. с постоянным во времени максимально возможным темпом роста
и неизменной структурой производства). В частности, в модели Неймана траектория ![]() является
магистралью
в пространстве интенсивностей технологических способов, а траектория
является
магистралью
в пространстве интенсивностей технологических способов, а траектория ![]() — магистралью в пространстве
выпусков продукции. Магистраль не зависит от длительности планового периода и
является эффективной
траекторией для любого конечного интервала времени.
— магистралью в пространстве
выпусков продукции. Магистраль не зависит от длительности планового периода и
является эффективной
траекторией для любого конечного интервала времени.
Применительно к широкому классу моделей экономической динамики доказываются теоремы о магистрали, утверждающие, что при достаточной продолжительности планового периода оптимальная траектория динамической модели независимо от начального состояния и целевой функции (или заданного конечного состояния) близка в том или ином смысле к магистрали. Модель, для которой справедлива теорема о магистрали, называют магистральной моделью.
Теоремы
о магистрали существуют в слабой, сильной и сильнейшей формах
(см. ДМНХ, с. 153 - 154). В частности, из теорем о магистрали в сильной и сильнейшей форме следует, что при любом начальном состоянии ![]() и
конечном состоянии
и
конечном состоянии ![]() (определяемых нормативно или с помощью целевой функции за период
[0, T] , так, что
(определяемых нормативно или с помощью целевой функции за период
[0, T] , так, что ![]() ) оптимальная
траектория состоит из трех участков: 1) движение от
) оптимальная
траектория состоит из трех участков: 1) движение от ![]() в
направлении магистрали; 2) движение по магистрали или в непосредственной
близости (параллельно) к ней; 3) движение от магистрали к
в
направлении магистрали; 2) движение по магистрали или в непосредственной
близости (параллельно) к ней; 3) движение от магистрали к ![]() (см.
рис. 11.3).
(см.
рис. 11.3).
|
|
Рис11.3. Оптимальная траектория и магистраль (для случая двух технологических способов или двух видов продукции).
Теоремы о магистрали утверждают, что продолжительность стартового и финишного участков траектории не зависит от длительности планового периода. Поэтому по мере увеличения планового периода все большая часть траектории будет проходить по магистрали или в непосредственной близости от нее. Таким образом, поведение оптимальной траектории при продолжительном плановом периоде зависит главным образом от структурных параметров модели и в меньшей степени от целевых функций, начальных и конечных условий[1].
Главным направлением обобщения и развития теоретических моделей расширяющейся экономики является расширение исходных допущений и условий с целью более полного отражения факторов экономического развития. В первую очередь следует отметить необходимость: 1) учета непроизводственного потребления, 2) включения ограниченных (невоспроизводимых или ограниченно воспроизводимых) ресурсов, 3) учета изменений во времени технологических матриц, отражающих научно-технический прогресс (о развиваемых в настоящее время подходах см. ДМНХ, с. 155 - 156; [4. Гл. 2,3]).
Построение обобщенных теоретических моделей расширяющейся экономики существенно облегчает анализ прикладных динамических моделей, придавая ему необходимую целеустремленность.
[1] Напомним, что в разд. 10.4 анализировались магистральные макроэкономические модели, в которых магистраль определяла максимальный темп роста и постоянные пропорции для таких показателей, как национальный доход, капитальные вложения, основные фонды потребления. Оптимальные траектории этих моделей с конечным интервалом времени также состоят из трех участков.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.