Лекция 10. Четырёхполюсники, реализованные на простейших пассивных и активных RC – цепях, - дифференцирующие и интегрирующие цепи
Четырёхполюсники, у которых выходное напряжение представляет собой производную (интеграл) напряжения на входе, называются дифференцирующими (интегрирующими) цепями. Основное назначение этих цепей – формирование электрических сигналов.
Дифференцирующие цепи позволяют производить следующие преобразования:
· получение производной по времени от сложных функций в вычислительных машинах, измерительной аппаратуре, системах авторегулирования;
· формирование остроконечных импульсов, служащих для запуска и синхронизации устройств импульсной техники;
· укорочение длительности импульсов;
· формирование прямоугольных импульсов из пилообразных.
Интегрирующие цепи позволяют производить следующие преобразования:
· получение интеграла по времени от сложных функций в измерительных схемах, системах авторегулирования;
· формирование импульсов, изменяющихся по линейному закону;
· увеличение времени импульсов.
Анализ общих свойств дифференцирующих и интегрирующих цепей, удобно проводить, используя аппарат передаточных функций и частотных характеристик, который позволяет установить функциональную связь выходной и входной величинами цепи.
Передаточной функцией четырехполюсника называется отношение
операторных изображений выходной ![]() и входной
и входной ![]() величин
величин
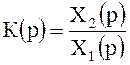 .
.
При заданной схеме соединений элементов четырехполюсника
передаточная функция определяется в результате расчета операторной схемы
замещения цепи при нулевых начальных условиях. Если функция ![]() и
и ![]() удовлетворяют
требованиям, при которых возможно преобразование Фурье, то, заменив
удовлетворяют
требованиям, при которых возможно преобразование Фурье, то, заменив ![]() =
=![]() в выражении
передаточной функции, получим частотную передаточную функцию
четырехполюсника
в выражении
передаточной функции, получим частотную передаточную функцию
четырехполюсника
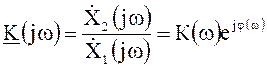 .
.
Функция ![]() , построенная на комплексной плоскости,
называется комплексной частотной характеристикой (КЧХ) четырехполюсника
и позволяет наглядно представить для каждой частоты входного сигнала отношение
амплитуд выходной и входной величин, а также сдвиг фаз между ними. Модуль КЧХ -
, построенная на комплексной плоскости,
называется комплексной частотной характеристикой (КЧХ) четырехполюсника
и позволяет наглядно представить для каждой частоты входного сигнала отношение
амплитуд выходной и входной величин, а также сдвиг фаз между ними. Модуль КЧХ -
![]() называется амплитудной частотной характеристикой (АЧХ)
четырехполюсника, а аргумент
называется амплитудной частотной характеристикой (АЧХ)
четырехполюсника, а аргумент ![]() называется фазовой частотной характеристикой (ФЧХ).
называется фазовой частотной характеристикой (ФЧХ).
10.2. Частотные характеристики пассивных дифференцирующих и интегрирующих цепей
Простейшие пассивные дифференцирующие цепи приведены на рис. 10.1. В соответствии с эквивалентными операторными схемами цепей при нулевых начальных условиях, находим
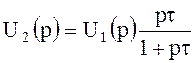 ,
,
где ![]() - постоянная времени цепи (
- постоянная времени цепи (![]() - для цепи рис. 10.1,а и
- для цепи рис. 10.1,а и ![]() - для цепи рис. 10.1,б).
- для цепи рис. 10.1,б).
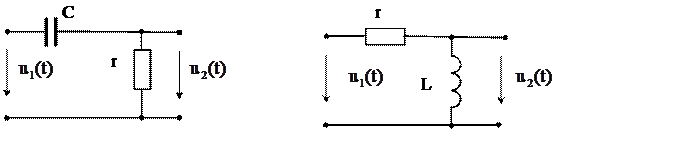 |
а) б)
Рис. 10.1
Передаточная функция цепей
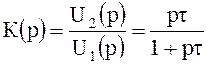 ,
,
а амплитудно-фазовая частотная характеристика
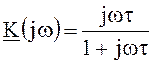 .
.
Таким образом, АЧХ и ФЧХ реального дифференцирующего четырехполюсника определяются:
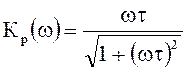 ;
; ![]() .
.
При условии wt<<1 амплитудно-фазовая частотная характеристика соответствует идеальному
дифференцирующему четырёхполюснику, для которого ![]() , и
соответственно АЧХ и ФЧХ идеального дифференцирующего четырехполюсника:
, и
соответственно АЧХ и ФЧХ идеального дифференцирующего четырехполюсника:
![]() ;
; ![]() .
.
Передаточная функция цепи в этом случае
![]() , т.е.
, т.е. ![]()
или, переходя к оригиналам,
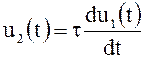 .
.
Логарифмическая амплитудная частотная характеристика (ЛАЧХ)
![]()
и
фазовая характеристика ![]() идеального
дифференцирующего четырехполюсника показана на рис. 10.2. Здесь указан наклон
ЛАЧХ (20
идеального
дифференцирующего четырехполюсника показана на рис. 10.2. Здесь указан наклон
ЛАЧХ (20 ![]() ) и частота среза -
) и частота среза - ![]() ,
при которой модуль характеристики
,
при которой модуль характеристики ![]() .
.
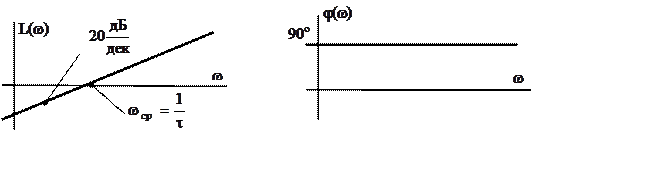 |
Рис. 10.2
Амплитудная частотная характеристика реального
дифференцирующего четырехполюсника ![]() отличается от
характеристики идеального дифференцирующего четырехполюсника
отличается от
характеристики идеального дифференцирующего четырехполюсника ![]() . Точность дифференцирования можно оценить
величиной относительного отклонения характеристик
. Точность дифференцирования можно оценить
величиной относительного отклонения характеристик ![]() и
и ![]()
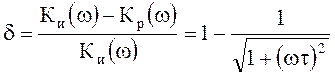 .
.
Отклонение d связано с
отклонением логарифмических амплитудных характеристик ![]() соотношением
соотношением
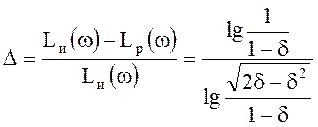 .
.
Выражение d показывает,
что с помощью простейших rC - и rL - цепей высокая точность
воспроизведения производной ![]() может быть получена
только в области сравнительно низких частот и малых постоянных времени цепи t, для которых wt<<1.
может быть получена
только в области сравнительно низких частот и малых постоянных времени цепи t, для которых wt<<1.
Попытка расширить диапазон частот качественного
дифференцирования за счет снижения постоянной времени цепи приводит к
существенному снижению выходного напряжения ![]() . В
области низких частот
. В
области низких частот
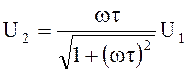 .
.
В случае если постоянная времени цепи ![]() задана или определена по известным
параметрам схемы, то при заданной точности дифференцирования
задана или определена по известным
параметрам схемы, то при заданной точности дифференцирования ![]() и допустимом снижении выходного напряжения
и допустимом снижении выходного напряжения
![]() диапазон частот
диапазон частот ![]() качественного
дифференцирования должен удовлетворять двум условиям:
качественного
дифференцирования должен удовлетворять двум условиям:
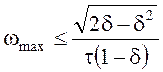 ;
; 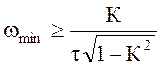 .
.
При выборе параметров четырехполюсника также
необходимо учесть ограничение по мощности источника сигнала ![]() . Полная мощность источника
. Полная мощность источника ![]() для цепи rC может
быть определена по соотношению
для цепи rC может
быть определена по соотношению
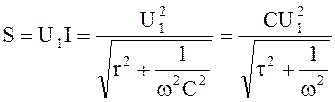 .
.
Для рассматриваемого диапазона частот ![]() S имеет наибольшее значение при
частоте
S имеет наибольшее значение при
частоте ![]() . При ограничении мощности источника
сигнала на уровне допустимого значения
. При ограничении мощности источника
сигнала на уровне допустимого значения ![]() величина
действующего значения источника сигнала
величина
действующего значения источника сигнала ![]()
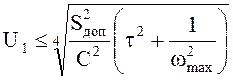 .
.
В случае цепи rL полная мощность источника определяется соотношением
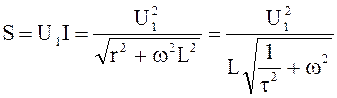
и
имеет наибольшее значение для частоты ![]() .
.
При ограничении ![]() на
уровне допустимого значения
на
уровне допустимого значения ![]() величина действующего
значения напряжения
величина действующего
значения напряжения ![]()
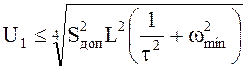 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.