Четырёхполюсники, реализованные на простейших пассивных и активных RC-цепях. Дифференцирующие и интегрирующие цепи, страница 4

или, переходя к оригиналу,

.

На интервале

,

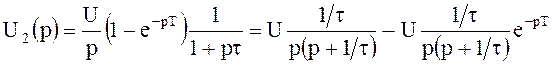или, переходя к оригиналу,

На рис. 10.12 показано изменение формы импульса  при изменении постоянной времени цепи  относительно длительности входного импульса  (рис. 10.12,а). Случай «б» соответствует режиму интегрирования. На практике достаточно точное интегрирование обеспечивается при выполнении условия . Случай «в» соответствует потери интегрирующих свойств.

В этом случае возможно использование электронного осциллографа в режиме периодической развертки, т.е. непосредственное наблюдение и снятие осциллограмм путем калькирования периодических кривых с экрана осциллографа.

 

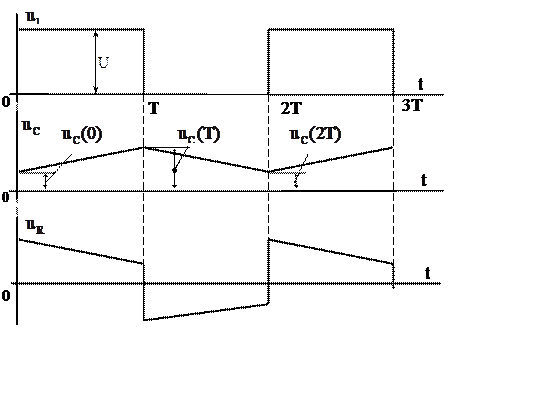Рис. 10.13

В случае экспериментального исследования свойств дифференцирующих и интегрирующих цепей при однократном воздействии прямоугольного импульса регистрация кривых выходного напряжения производится путем записи кривых на фотопленку (фотобумагу) с помощью светолучевых осциллографов или путем фотографирования изображения с экрана электронного осциллографа, обладающего послесвечением. Ввиду трудоемкости данных способов, исследование указанных свойств цепей удобнее проводить при воздействии периодических прямоугольных импульсов. Как следует из описания процессов в дифференцирующих цепях при воздействии одиночного прямоугольного импульса, режим точного дифференцирования будет эквивалентен этому же режиму при воздействии периодических прямоугольных импульсов, так как длительность переходного процесса в цепи << T, и к моменту появления каждого импульса начальные условия в схеме являются нулевыми

.

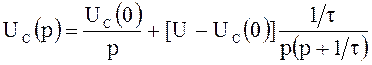Заметив, что условие переходной цепи, передающей импульс без искажения, и условие точного интегрирования совпадают , а отличие заключается в том, с какого элемента снимается выходное напряжение, проведем анализ цепи при воздействии периодических прямоугольных импульсов. Рассмотрим цепь . Качественный характер процессов приведен на рис. 10.13. Так как начальные условия к моменту появления импульса не нулевые, операторная схема цепи для интервала  будет иметь вид рис. 10.14,а.

Переходя к оригиналу, получим соотношение для интервала

.

 

а)                                                                                       б)

Рис. 10.14

На момент времени  находим напряжение на конденсаторе , которое является начальным значением для второго интервала

.

На интервале  входное напряжение равно нулю, и операторная схема имеет вид рис. 10.14, б, рассчитывая которую, получаем

,

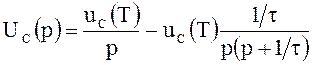и, следовательно, на интервале

.

На момент времени

.

При установившемся процессе

.

Подставляя  в выражение для напряжения , находим

.

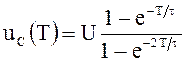Учитывая, что , с точностью до 2,5 % можно ограничиться первыми двумя членами в разложении экспоненциальной функции в степенной ряд и получить приближенное выражение для напряжения . При этом, , и напряжение  изменяется по линейным законам:

         для интервала

;

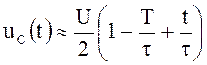          для интервала 

.

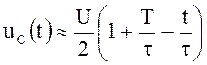Напряжение 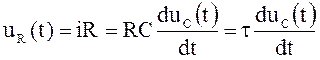 на интервалах постоянно:

          для интервала            ;

          для интервала          .

Таким образом, кривая  представляет собой периодические разнополярные прямоугольные импульсы с амплитудой . Это положение может быть принято как критерий настройки дифференцирующей цепи на режим переходной цепи и как критерий настройки интегрирующей цепи  на режим точного интегрирования при воздействии на цепь периодических однополярных прямоугольных импульсов.