Четырёхполюсники, реализованные на простейших пассивных и активных RC-цепях. Дифференцирующие и интегрирующие цепи, страница 2

При дифференцировании сложных периодических функций требуемый диапазон частот  устанавливается на основании разложения функции в ряд Фурье и ограничения спектра высшей гармоникой, еще имеющей существенное значение для формы импульсов   на выходе цепи. Вид простейших пассивных интегрирующих цепей приведён на рис. 10.3. Передаточная функция и амплитудно-фазовая частотная характеристика этих цепей определятся соотношениями:

 ;                .

 

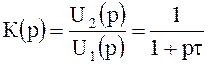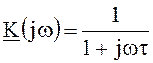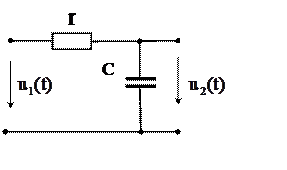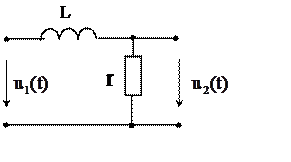Рис. 10.3

АЧХ и ФЧХ  реальной  интегрирующей  цепи определяются соотношениями:

;          .

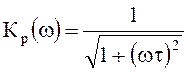При условии wt>>1 амплитудно-фазовая частотная характеристика соответствует идеальной интегрирующей цепи, для которой

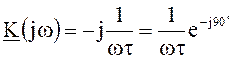
и, соответственно, АЧХ и ФЧХ идеального интегрирующего четырехполюсника:

 ;      .

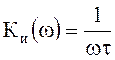Передаточная функция цепей для этого случая:

;              

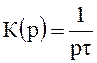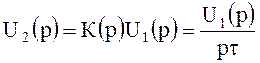
или, переходя к оригиналам,   .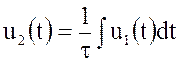

Логарифмическая амплитудно-частотная и фазовая характеристики идеального интегрирующего четырехполюсника:

;       .

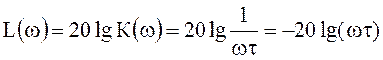Графики этих зависимостей показаны на рис. 10.4.

 

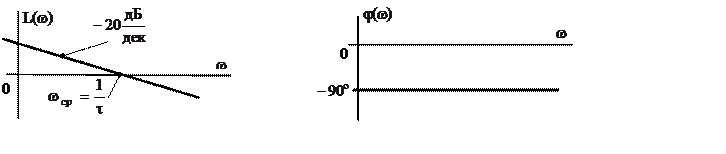Рис. 10.4

Точность интегрирования можно оценить величиной относительного отклонения амплитудной частотной характеристики  реального интегрирующего четырехполюсника  от соответствующей характеристики идеального интегрирующего четырехполюсника

.

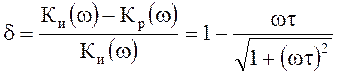Величина d связана с отклонением логарифмических амплитудных  характеристик соотношением

.

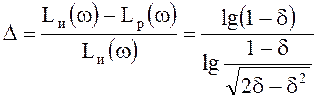С помощью простейших  - и   - цепей высокая точность воспроизведения интеграла  может быть получена только в области сравнительно высоких частот и больших постоянных времени цепей wt>>1. Попытка расширить диапазон частот качественного интегрирования за счет повышения постоянной времени цепи приводит к существенному снижению выходного напряжения

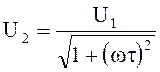
в области высоких частот. Диапазон частот интегрирования определяется исходя из требуемой точности интегрирования  и допустимого снижения выходного напряжения :

;   .

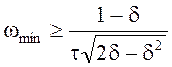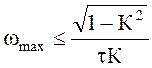Действующее значение напряжения  на входе интегрирующего четырехполюсника определяется из условия ограничения источника сигнала по мощности . Величина напряжения  находится так же, как и для дифференцирующих цепей.

Следует заметить, что в настоящее время дифференцирующие и интегрирующие четырехполюсники с индуктивностью практически не применяются, так как активное сопротивление катушек и паразитная (межвитковая) емкость не позволяют получить требуемую точность операций. В данном разделе исследуются только дифференцирующие и интегрирующие четырехполюсники, реализованные на rC - цепях.

10.3. Частотные характеристики активных дифференцирующих и интегрирующих цепей

К главным недостаткам пассивных дифференцирующих и интегрирующих четырехполюсников следует отнести, прежде всего, малый коэффициент передачи  и относительно узкий частотный диапазон ().

 

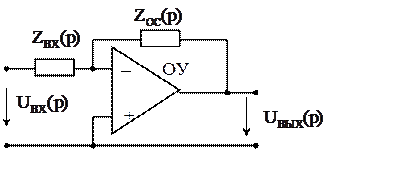Рис. 10.5

Лучшие результаты можно получить с помощью активных дифференцирующих и интегрирующих четырехполюсников, содержащих операционный усилитель (ОУ). Цепь, собранная на активных элементах обладает более высоким коэффициентом передачи и широким частотным диапазоном. Простейшая цепь, содержащая операционный усилитель с элементом обратной связи показана на рис. 10.5.

Как правило, ОУ имеют два входа и один выход. Входные выводы обозначены знаками «плюс» и «минус». Знак «плюс» означает, что выходное напряжение совпадает по знаку с входным напряжением (входное и выходное напряжение совпадает по фазе). Поэтому входной вывод «плюс» называется не инвертирующим. Входной вывод «минус» является инвертирующим. На рис. 10.6 показана эквивалентная схема для уровней входных напряжений, при которых ОУ можно рассматривать как линейный четырёхполюсник.