Приложение
Аналитическое решение системы двух линейных дифференциальных уравнений первого порядка в среде MathCad
Найдём решение неоднородной системы двух линейных дифференциальных уравнений второго порядка, записанной в нормальной форме (форме Коши):
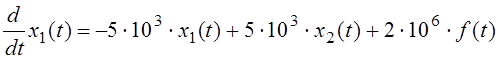
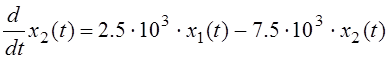
при нулевых начальных условиях
![]() и
и ![]() ,
,
в которой
![]() .
.
Решение.
Интегрируя каждое уравнение этой системы в пределах от 0– до 0+, получаем стартовые значения x1(0+) è x2(0+) искомых функций:
x1(0+) = x1(0–) = 0,
x2(0+) = x2(0–) = 0.
При t ³ 0 функции x1(t)
è x2(t) представим суммой принуждённых ![]() ,
,
![]() и свободных
и свободных ![]() ,
, ![]() составляющих:
составляющих:
![]() ,
,
![]() ,
,
известных в математике как частное решение неоднородной системы уравнений и общее решение однородной системы уравнений соответственно.
Поскольку
![]() ,
,
где ![]() , а w = 2000 рад/с,
, а w = 2000 рад/с,
то частное решение исходной системы уравнений ищем в такой же форме:
![]() ,
, ![]()
где ![]() и
и
![]()
комплексные
амплитуды гармонических функций ![]() и
и ![]() .
.
Подставляя эти предполагаемые выражения принуждённых
составляющих искомых функций в исходную систему дифференциальных уравнений,
сбрасывая операторы Re в правой и левой её частях и сокращая затем обе части
уравнений на экспоненциальный множитель ![]() ,
получаем следующую систему алгебраических уравнений, определяющую значения
комплексных амплитуд X1m и X2m
гармонических функций
,
получаем следующую систему алгебраических уравнений, определяющую значения
комплексных амплитуд X1m и X2m
гармонических функций ![]() и
и ![]() :
:
![]()
![]() .
.
Решим эту систему уравнений в среде MathCad.
Пусть ![]() , w = 2000 рад/с,
, w = 2000 рад/с,
Given
![]()
![]() .
.
(Здесь левые и правые части уравнений связаны знаком эквивалентности – жирным знаком “равно” панели Boolean, вводимым клавишей “ = ” при нажатой клавише “ Ctrl ”).
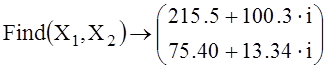
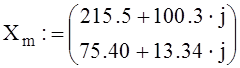
![]()
![]()
![]() рад
рад
![]()
![]()
![]() рад
рад
![]()
![]()
![]()
![]()
![]()
![]()
Найдём, далее, общее решение однородной системы уравнений
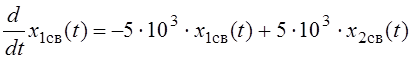
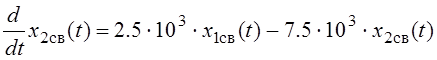 .
.
В протоколе документа MathCad запишем матрицу А этой системы уравнений:
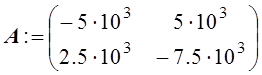
и вычислим вектор p её характеристических чисел:
![]()
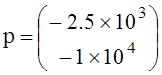 .
.
Получим также матрицу V значений собственных векторов матрицы системы уравнений А:
![]()
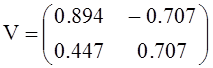
Следовательно, выражения свободных составляющих искомых функций могут быть записаны в таком виде
![]() ,
,
![]() .
.
Значения постоянных интегрирования D1 и D2 находятся по стартовым значениям искомых функций x1(0+) и x2(0+).
Запишем выражения искомых функций при t ³ 0:
![]() ,
,
![]() .
.
Отсюда, в частности, при t = 0 получаем
![]() ,
,
![]() .
.
Первый способ определения значений постоянных интегрирования D1 и D2:
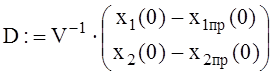
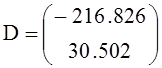 .
.
Вычислим значения коэффициентов перед экспонентами ![]() и
и ![]() выражений
искомых функций и их свободных составляющих
выражений
искомых функций и их свободных составляющих
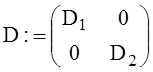
![]()
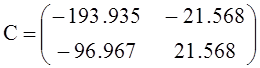
либо
![]()
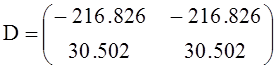
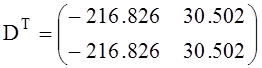
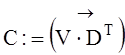
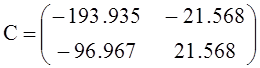
Здесь “®” символ оператора векторизации – поэлементного перемножения элементов двух матриц; вводится клавишей “ – ” при нажатой клавише “ Ctrl ”.
Второй способ определения значений постоянных интегрирования
Given
![]()
![]()
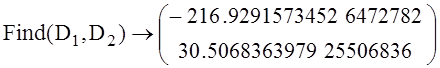
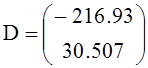
Вычислим значения коэффициентов перед экспонентами ![]() и
и ![]() выражений
искомых функций и их свободных составляющих
выражений
искомых функций и их свободных составляющих
![]()
![]()
![]()
![]()
Следовательно,
![]() ,
,
![]() .
.
Внимание!
Значения постоянных интегрирования можно также найти по стартовым значениям
переменных состояния цепи x1(0+),
x20+) и их первых
производных ![]() ,
, ![]() .
.
В протоколе документа MathCad запишем матрицу А однородной системы двух линейных дифференциальных уравнений:
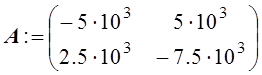
и вычислим вектор p её характеристических чисел:
![]()
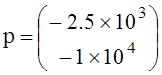 .
.
Следовательно, выражения свободных составляющих искомых функций могут быть записаны в таком виде
![]() ,
,
![]() .
.
Для вычисления значений постоянных интегрирования,
например, C11 и C12 выражения
свободной составляющей x1св(t) воспользуемся
стартовыми значениями этой функции x1св(0+) и её первой производной ![]() .
.
Из принятого представления искомой функции x1(t) при t ³ 0
![]()
при t = 0+ имеем:
![]() ,
,
![]()
Стартовое значение искомой функции x1(t)
было определено ранее: x1(0+) = 0. Стартовое значение
её производной ![]() определяется значением правой
части первого уравнения исходной неоднородной системы двух линейных
дифференциальных уравнений при t = 0+:
определяется значением правой
части первого уравнения исходной неоднородной системы двух линейных
дифференциальных уравнений при t = 0+:
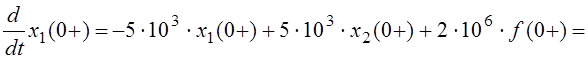
![]() .
.
Следовательно
![]() ;
;
![]() .
.
Таким образом, для вычисления значений постоянных интегрирования C11 и C12 имеем следующую систему алгебраических уравнений:
![]() ,
,
![]() .
.
Решим её в программе MathCad.
Given
![]()
![]()
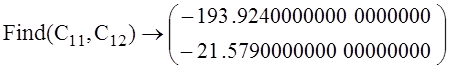
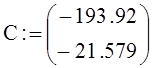 .
.
Следовательно,
![]() .
.
Таким же образом определяются значения постоянных
интегрирования C21 и C22 выражения ![]() свободной составляющей искомой функции
свободной составляющей искомой функции ![]() .
.
В заключении решения этой задачи запишем окончательные выражения искомых функций при t ³ 0 в виде сумм их принуждённых и свободных составляющих
![]() ,
,
![]() .
.
Проверка: Стартовые значения найденных функций x1(t) и x2(t)
x1(0+) = 0, x2(0+) = 0,
как и должно быть в соответствии с условием этой задачи.
D:\ОТЦиС\Упражнения\Тема_6c\Примеры_6c\Пример 0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.