Вариант № 15
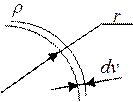 Условия задачи: В
цилиндрическом диэлектрике длиной один метр. Суммарный заряд системы состоит из
совокупностей объёмных зарядов в областях 1 и 2
Условия задачи: В
цилиндрическом диэлектрике длиной один метр. Суммарный заряд системы состоит из
совокупностей объёмных зарядов в областях 1 и 2 ![]() и
и ![]() , а также поверхностных, которые с
плотностью
, а также поверхностных, которые с
плотностью ![]() и
и ![]() располагаются
на цилиндрических плоскостях с заданными значениями радиусов.
располагаются
на цилиндрических плоскостях с заданными значениями радиусов.
Если заряд распределён в объёме с
плотностью ![]() , например если в качестве элемента объёма dV выбрать тонкую цилиндрическую
оболочку с радиусом r, длиной l,
и толщиной dv, то заряд в объёме, ограниченный
поверхностями r1 и r2,
а если в этом объёме величина заряда неизменна, то заряд равен
, например если в качестве элемента объёма dV выбрать тонкую цилиндрическую
оболочку с радиусом r, длиной l,
и толщиной dv, то заряд в объёме, ограниченный
поверхностями r1 и r2,
а если в этом объёме величина заряда неизменна, то заряд равен ![]()
Определить:
Дано:
Рисунок 1-3
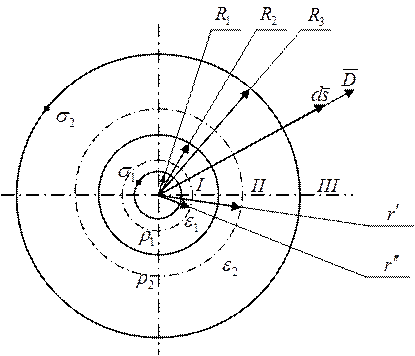
![]()
![]()
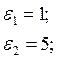
Система пространственных тел
цилиндрической формы, содержит неподвижные электрические заряды. В областях I и II имеются пространственные заряды, расположенные в
диэлектрических средах с диэлектрической проницаемостью ![]() и
и
![]() соответственно. Вне системы среда имеет
диэлектрическую проницаемость
соответственно. Вне системы среда имеет
диэлектрическую проницаемость ![]() .
.
Суммарный заряд состоит из
совокупности объёмных зарядов в области I и в области II, в качестве элемента объёма будем брать тонкую
цилиндрическую оболочку радиуса r, длиной l и толщиной dr, тогда получим ![]() , где
, где ![]() и,
следовательно,
и,
следовательно, ![]()
Определяем суммарный заряд системы:
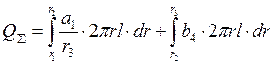 ;
;
где ![]() - объёмная плотность;
- объёмная плотность;
l – длина цилиндра;
r – радиус цилиндра.
Для областей I,
II и III рассчитать системы по теореме Гаусса ![]() рассчитаем
распределение вектора смещения - поток вектора смещения через любую замкнутую
поверхность равен полному свободному заряду находящемуся в объёме ограниченном
этой замкнутой поверхностью.
рассчитаем
распределение вектора смещения - поток вектора смещения через любую замкнутую
поверхность равен полному свободному заряду находящемуся в объёме ограниченном
этой замкнутой поверхностью.
Область III:
Заряд области равен суммарному
заряду системы ![]() , так как радиус рассматриваемой
области больше радиуса системы.
, так как радиус рассматриваемой
области больше радиуса системы.
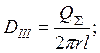
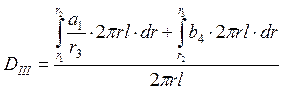
Область II:
Поверхность области II охватывает заряд области I с объёмной плотностью ![]() и часть
заряда области II с радиусом
и часть
заряда области II с радиусом ![]() и
объемной плотностью
и
объемной плотностью ![]() , следовательно, равен:
, следовательно, равен:
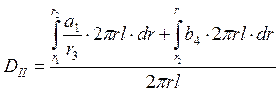
Область I:
Поверхность области I охватывает часть заряда области I,
верхним пределом которого является текущий радиус ![]() :
:
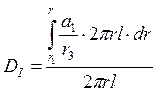 ;
;
На качественном уровне графики можно построить не решая задачу, а руководствуясь, законами и положениями электростатики. Таковыми, в частности, являются:
- принцип потенциальности: ![]() ;
;
- теорема Гаусса: ![]()
Из этих законов могут быт получены зависимости, связывающие значения компонентов векторов на границах раздела сред с различными физическими свойствами. Эти зависимости называют граничными условиями.
Построим график D(r):
При решении задачи в общем виде график можно построить на качественном уровне, руководствуясь законами и положениями в области электростатики, таковыми являются:
- принцип потенциальности циркуляции по замкнутой поверхности;
- теорема Гаусса.
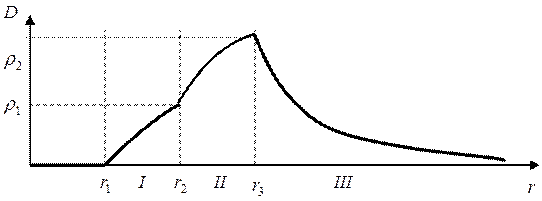
Построим график E(r):
Отличительной особенностью этого
графика является наличие скачков на границах областей, из-за разности
диэлектрических постоянных сред. Если на пассивной границе ![]() остаётся непрерывной. То нормальная
составляющая -
остаётся непрерывной. То нормальная
составляющая - ![]() обязательно терпит разрыв. При
этом обязательно выполняется равенство
обязательно терпит разрыв. При
этом обязательно выполняется равенство 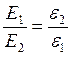
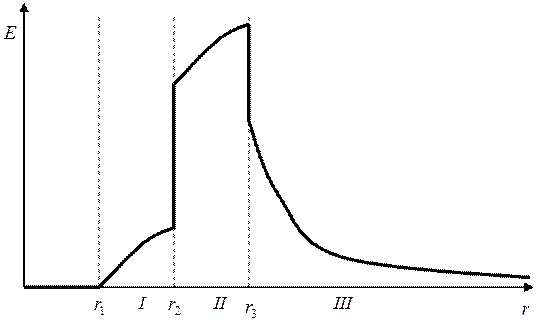
Построим график φ(r):
Так как функция φ представляет
собой: 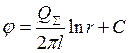 , следовательно, график непрерывно
возрастает с увеличением радиуса и устремляется в бесконечность. В этом графике
не может быть скачков, разрывов, т.к. потенциал - есть функция энергетическая,
поэтому она и в пространстве и во времени всегда непрерывна.
, следовательно, график непрерывно
возрастает с увеличением радиуса и устремляется в бесконечность. В этом графике
не может быть скачков, разрывов, т.к. потенциал - есть функция энергетическая,
поэтому она и в пространстве и во времени всегда непрерывна.
Если в области ![]() , то
, то ![]() в этой
области.
в этой
области.
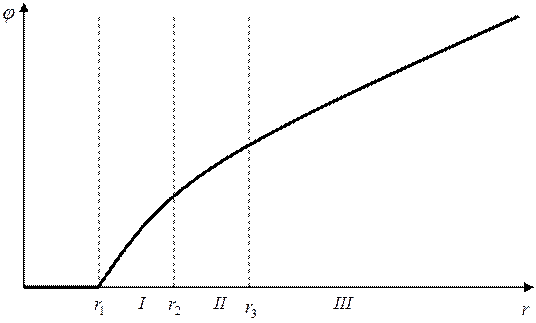
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.