Задача 2
|
Рис. 1 |
Определите выражения токов i1(t) и i2(t) резисторов R1 и R2 в схеме цепи Рис. 1 после коммутации и постройте их графики, если Uo1 = 100 В, R1 = 500 Ом, Uo2 = 50 В, R2 = 500 Ом, C3 = 10 мкФ, C4 = 40 мкФ. |
Решение.
|
Рис. 2 |
Совместим начало отсчёта относительного времени t (t = 0) с моментом коммутации в цепи Рис. 1. По умолчанию эта цепь до коммутации (t < 0) находится в стационарном состоянии. Из схемы цепи в стационарном состоянии (Рис. 2) находим начальные значения напряжений конденсаторов u3(0–) и u4(0–), т. е. их значения накануне коммутации (t = 0–) *
|
|
|
|
Рис. 3 |
Рис. 4 |
u3(0–) = Uo1 = 100 В, u4(0–) = – Uo2 = – 50 В.
В качестве переменной состояния (независимой переменной) цепи после коммутации (Рис. 3) выберем напряжение одного из двух конденсаторов, например, напряжение u3(t) конденсатора C3. В этом случае напряжение u4(t) конденсатора C4 станет зависимой переменной цепи, являющейся линейной функцией переменной состояния
u3(t) = u4(t).
Составим затем уравнение состояния цепи после коммутации, в котором искомой функцией будет переменная состояния цепи – напряжение u3(t) конденсатора C3. Считая известным выражение его мгновенного значения и опираясь на принцип компенсации ** , изобразим схему замещения цепи для произвольного момента времени t ³ 0. Для схемы цепи Рис. 3 в результате такой замены получим схему замещения, как на Рис.4. Из неё находим выражение тока i3(t) конденсатора C3:
i3 = i1 + i2 – i4
или, поскольку u1(t) = Uo1 – u3(t), u2(t) = – (Uo2 + u4(t)),
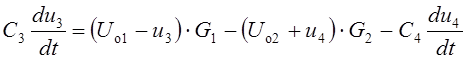 .
.
Интегрируя это выражение в пределах от 0– до 0+, получаем соотношение между начальными u3(0–), u4(0–) и стартовыми u3(0+), u4(0+) значениями напряжений конденсаторов
![]() .
.
С учётом равенства стартовых значений напряжений конденсаторов
u3(0+) = u4(0+)
находим
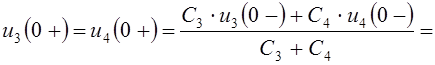
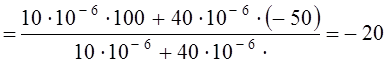 В.
В.
Как видим, значения напряжений конденсаторов изменились скачком. Нетрудно показать, что конечное изменение значений напряжений конденсаторов за бесконечно малое время коммутации обусловлено бесконечно короткими импульсами бесконечно больших токов конденсаторов *. Действительно, значения токов конденсаторов i3(0) и i4(0) в момент коммутации:
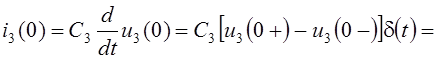
![]() А,
А,
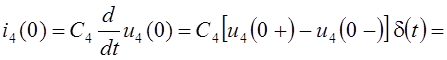
![]() А.
А.
Таким образом, конденсатор C3 мгновенно разряжается (i3(0) < 0), а конденсатор C4 мгновенно заряжается (i4(0) > 0) одинаковыми токами от различных начальных значений напряжений u3(0–) = 100 В, u4(0–) = – Uo2 = – 50 В до одинаковых стартовых значений напряжений u3(0+) = u4(0+) = – 20 В.
До коммутации энергия конденсаторов равна
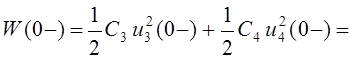
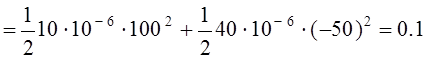 Дж.
Дж.
После коммутации энергия обоих конденсаторов
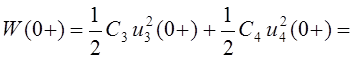
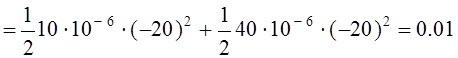 Дж
Дж
стала меньше. Очевидное нарушение закона сохранения энергии в рассматриваемой задаче объяснить невозможно.
Вернёмся к выражению
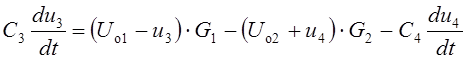 .
.
Отсюда, после несложных преобразований, учитывая равенство напряжений конденсаторов u3(t) = u4(t) при t ³ 0, получаем искомое уравнение состояния цепи, записанное в нормальной форме (форме Коши):
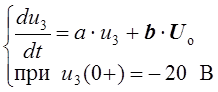 .
.
Здесь
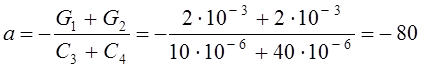 с-1;
с-1;
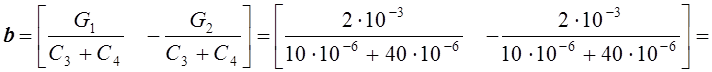
![]() с-1.
с-1.
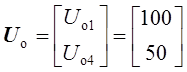 В
В
Далее задачу решаем в два этапа. Сначала получим выражение переменной состояния цепи u3(t) (независимой переменной) после замыкания ключа (при t ³ 0), а затем для тех же моментов времени t получим выражение искомых зависимых переменных – токов i1(t) и i2(t) резисторов R1 и R2 в схеме цепи Рис. 3.
I этап. При t ³ 0 напряжение u3(t) конденсатора C3 представим суммой двух составляющих
![]() ,
,
где
![]() –
принуждённая составляющая напряжения конденсатора C3, совпадающая с его установившимся значением;
–
принуждённая составляющая напряжения конденсатора C3, совпадающая с его установившимся значением; ![]() – свободная
составляющая напряжения конденсатора.
– свободная
составляющая напряжения конденсатора.
|
Рис. 5 |
Из схемы цепи после коммутации в стационарном состоянии (Рис. 5) находим
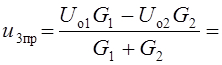
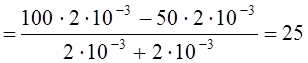 В
В
Для составления выражения свободной составляющей напряжения u3(t) конденсатора C3 получим сначала характеристическое уравнение цепи и найдём его корни. Обращаясь к уравнению состояния цепи, записываем его характеристическое уравнение
![]() ,
,
единственный корень которого равен
![]() с-1.
с-1.
Отметим попутно, что значение постоянной времени t цепи равно
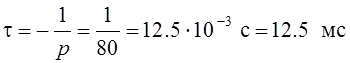 .
.
При единственном корне характеристического уравнения
![]() В.
В.
В соответствии с принятым представлением при t ³ 0 напряжение конденсатора C3
![]() .
.
Полагая здесь t = 0+, находим
![]() В.
В.
Следовательно, напряжение конденсатора u3(t) в цепи после коммутации (Рис. 3) представляется выражением:
![]() В при t ³ 0.
В при t ³ 0.
II этап. Выражение напряжения u4(t) конденсатора C4 в цепи после коммутации (Рис. 6.3)
![]() В при t ³ 0.
В при t ³ 0.
Запишем выражения искомых токов i1(t) и i2(t) резисторов R1 и R2 в схеме цепи Рис. 6.3
![]() А,
А,
![]() А.
А.
Проверка:
Проверим, соблюдается ли баланс токов элементов исследуемой цепи в независимом, например, верхнем узле схемы (Рис. 6.3):
![]()
При известном выражении напряжения конденсатора u3(t) зависимость его тока i3(t) от времени определяется его динамической характеристикой:
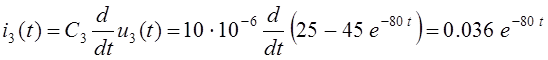 А.
А.
Аналогичным образом находится выражение тока конденсатора C3:
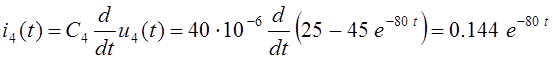 А,
А,
Следовательно,
![]()
![]()
Полученные выражения токов элементов цепи после коммутации удовлетворяют ограничению, налагаемому первым законом Кирхгофа.
Зависимости i1(t) и i2(t) на интервале 0 £ t £ 60 мс с шагом 6 мс представлены в таблице и на Рис. 6.
Таблица
|
t, мс |
0 |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
56 |
60 |
|
i1(t), А |
0.24 |
0.206 |
0.184 |
0.171 |
0.163 |
0.158 |
0.155 |
0.153 |
0.152 |
0.151 |
0.151 |
|
i2(t), А |
-0.06 |
-0.094 |
-0.116 |
-0.129 |
-0.137 |
-0.142 |
-0.145 |
-0.147 |
-0.148 |
-0.149 |
-0.149 |
|
Рис. 6 |
Численное решение этой задачи осуществляется также в указанные два этапа.
Обратимся сначала к полученному ранее уравнению для переменной состояния цепи в виде
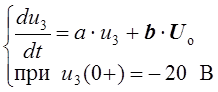 ,
,
в котором
a = – 80 с-1, ![]() с-1.
с-1.
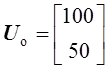 В
В
Результаты численного и аналитического исследования переходного процесса в рассматриваемой цепи полностью совпадают, по крайней мере до трёх цифр после запятой мантисс мгновенных значений токов i1(t) и i2(t) резисторов R1 и R2.
* Напомним, что конденсатор в стационарном состоянии эквивалентен разъёму.
** Любой элемент с известным значением напряжения может быть эквивалентно заменён источником напряжения известного значения.
* Токов, выражаемых через d-функцию (функцию Дирака) d(t) = s¢(t).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.