Определение выражения тока катушки в схеме RL-цепи первого порядка после коммутации

Классический анализ переходных процессов в RL-цепях

первого порядка

Задача 6.0

Решение.

Совместим момент коммутации в цепи Рис. 6.1 с началом отсчёта относительного времени t в ней, то есть с одним из моментов времени t = 0, когда

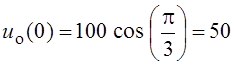 В,                   .

Из схемы цепи до коммутации Рис. 6.1 видно, что начальное – накануне коммутации (t = 0–) – значение тока катушки равно нулю

 .

Из схемы цепи после коммутации (Рис. 6.2) на основании второго закона Кирхгофа имеем условие

.

Подставляя сюда выражение динамической характеристики катушки

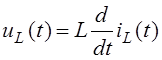
получаем дифференциальное уравнение для тока катушки i_L(t) в цепи после коммутации (Рис. 6.2):

.

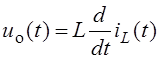Интегрируя его в пределах от 0– до 0+, получаем соотношение между начальным i_L(0–) и стартовым i_L(0+) значениями тока катушки L

i_L(0+) = i_L(0–) = 0.

Выражение тока катушки i_L(t) при t ³ 0 можно найти непосредственным интегрированием дифференциального уравнения

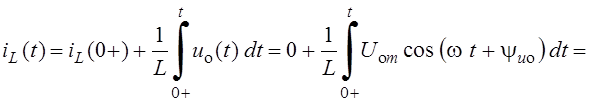
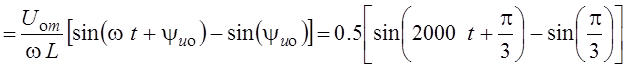 А.

Если раскрыть здесь квадратные скобки, то первое слагаемое представляет собой выражение принуждённой (гармонической) составляющей тока катушки

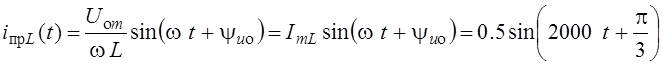 А.

Второе (постоянное) слагаемое является значением незатухающей свободной составляющей тока катушки

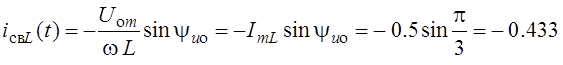 А.

Такая особенность свободной составляющей тока катушки объясняется тем, что единственный элемент цепи, освобождённой от источника напряжения, – катушка – не потребляет энергии.

Зависимости нормированных значений задающего напряжения 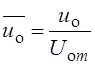, тока катушки  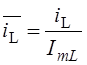и его принуждённой 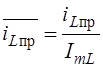 и свободной  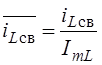составляющих на интервале времени 0 £ t £ 5 мс показаны на Рис. 6.3.

Знак значения свободной составляющей тока катушки определяется значением начальной фазы y_uo задающего напряжения, то есть фактически от момента коммутации. А если y_uo равно 0 или p, то свободная составляющая тока катушки вообще отсутствует

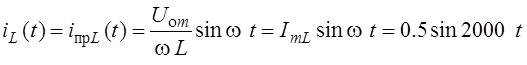 А.

Иными словами, если ключ в цепи Рис. 6.1 замыкается в те моменты времени, когда принуждённая составляющая тока катушки i_Lпр(t) обращается в нуль, то после коммутации сразу установится гармонический процесс.

Решим эту же задачу численно.

Обратимся сначала к полученному ранее уравнению для тока i_L(t) катушки цепи после коммутации в несколько изменённом виде

,

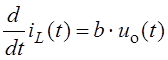при                                               ;

Здесь 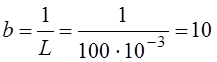                        См/с.

Численное решение уравнения для тока i_L(t) катушки цепи при 0 £ t£ 5 мс найдём с помощью функции rkfixed математического пакета MathCad 2000 Pro, реализующей метод Рунге-Кутта с фиксированным шагом. После ввода исходных данных задачи устанавливаем значение ORIGIN = 0 и задаём:

                       – выражение первой производной  тока катушки i_L(t);

  – вычисление значений элементов матрицы тока катушки i_L(t) в пятистах точках (500) интервала времени [0,0.005] с;

                            – номера точек разбиения интервала времени [0,0.005] с пробегают значения от 0 до числа строк без 1 матрицы Z.

                                        – элементам вектора t присваивают значения элементов первого столбца матрицы Z;

                                       – элементам вектора i_L(t)  присваивают значения элементов второго столбца матрицы Z;

Результаты численного и аналитического исследования переходного процесса в рассматриваемой цепи на интервале 0 £ t£ 5 мс полностью совпадают, по крайней мере до трёх значащих цифр мантиссы мгновенных значений тока катушки i_L(t).

Рассмотренная простейшая задача является, конечно, довольно грубой моделью переходного процесса в неразветвлённой цепи с катушкой. Однако её анализ даёт выражение тока катушки, значения которого приемлемы при малых значениях относительного времени. Чтобы установить пределы применимости такой модели придётся исследовать более сложные модели, учитывающие, например, диссипативные свойства реальной катушки (Рис. 6.4) и ёмкостный эффект (межвитковую ёмкость) (Рис. 6.5).

D:\ОТЦиС\Упражнения\Тема_6a\Примеры_6a\Пример 0