Классический анализ переходных процессов в RC-цепях
второго порядка
Задача 6.2
|
Рис. 6.1 |
Определите выражения напряжений конденсаторов u1(t), u2(t) и u3(t) в схеме цепи Рис. 6.1 после одновременной коммутации трёх ключей и постройте их графики, если Uo = 90 В, C1 = C2 = C3 = 3 мкФ, R4 = R5 = 1 кОм. |
Решение.
Совместим начало отсчёта относительного времени t с моментом синхронной коммутации в цепи Рис. 6.1.
|
Рис. 6.2 |
В качестве переменных состояния (независимых переменных) цепи после коммутации ключей (при t ³ 0) выберем напряжения конденсаторов u1(t), u2(t) и u3(t). Для определения их начальных значений u1(0–), u2(0–) и u3(0–) обратимся как обычно к схеме цепи накануне коммутации в стационарном состоянии (Рис. 6.2) (*). Однако, из этой схемы искомые значения трёх величин не могут быть вычислены однозначно, поскольку они ограничены единственным условием – вторым законом Кирхгофа:
u1(0–) + u2(0–) + u3(0–) = Uo.
|
Рис. 6.3 |
Начальные значения напряжений конденсаторов u1(0–), u2(0–) и u3(0–) можно найти, анализируя результат коммутации в схеме цепи, приведшей к образованию цепи Рис. 6.2. Так, например, если три одинаковых незаряженных конденсатора C1, C2 и C3, соединённые последовательно, подключаются к источнику постоянного напряжения Uo (Рис. 6.3), то каждый из них мгновенно зарядится до напряжения Uo/3. Именно этот вариант и рассматривается в дальнейшем.
Итак, положим начальные значения напряжений конденсаторов u1(0–), u2(0–) и u3(0–) накануне коммутации в схеме цепи (Рис. 6.1) одинаковыми и равными
u1(0–) = u2(0–) = u3(0–) = Uo/3 = 30 В.
Нетрудно показать, что выражения переменных состояния u1(t), u2(t) и u3(t) цепи после коммутации (Рис. 6.4) (при t ³0) связаны однородной системой трёх линейных дифференциальных уравнений первого порядка:
|
Рис. 6.4 |
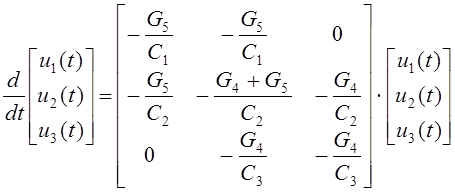 .
.
Интегрируя их в пределах от 0– до 0+, получаем соотношения между начальными u1(0–), u2(0–), u3(0–) и стартовыми u1(0+), u2(0+), u3(0+) значениями напряжений конденсаторов, выражающие второй закон коммутации:
u1(0+) = u1(0–) = 30 В,
u2(0+) = u2(0–) = 30 В,
u3(0+) = u3(0–) = 30 В.
Далее задача решается по известному алгоритму (см. например, решение предыдущей задачи 6.1).
|
Рис. 6.5 |
Порядок системы уравнений для переменных состояния цепи после коммутации (Рис. 6.4) можно уменьшить на единицу (сократить до двух), если использовать присущее этой цепи особое свойство – симметрию относительно конденсатора C2. Для большей наглядности на Рис. 6.5 изображена схема цепи, изоморфная рассматриваемой схеме (Рис. 6.4), в которой
R4 = R5, C1 = C3
(это необходимые, но недостаточные условия) и не менее важные ограничения
u1(0+) = u3(0+).
На Рис. 6.6 показана схема цепи, эквивалентная предыдущей. Значения токов проводов aa¢ и bb¢, пересекающих ось симметрии, очевидно равны нулю, поэтому их можно заменить также разъёмами aa¢ и bb¢ (Рис. 6.7).
|
|
|
|
Рис. 6.6 |
Рис. 6.7 |
Таким образом, анализ переходного процесса в симметричной схеме цепи третьего порядка Рис. 6.4 благодаря одинаковым стартовым значениям напряжений конденсаторов C1 и C3 сводятся, по существу, к анализу переходного процесса в одной из двух одинаковых цепей второго порядка (Рис. 6.7).
|
Рис. 6.8 |
Подобная задача решена в предыдущем примере (задача 6.1), поэтому здесь мы приведём лишь искомые выражения переменных состояния цепи Рис. 6.1 при t ³ 0 и их графики (Рис. 6.8):
![]() В;
В;
![]() В;
В;
![]() В.
В.
Проверка:
При известном выражении напряжения конденсатора u1(t) зависимость его тока i1(t) от времени определяется динамической характеристикой конденсатора C1:
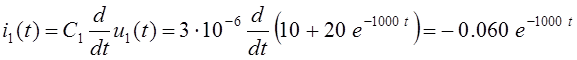 А.
А.
Аналогичным образом найдём выражения токов i2(t) и i3(t) второго и третьего конденсаторов:
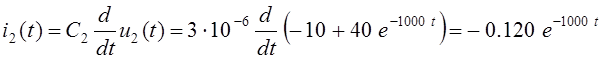 А,
А,
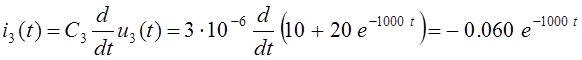 А.
А.
Из анализа схем цепи после коммутации Рис. 6.4 или Рис. 6.5 следует
![]() ,
,
как и должно быть в соответствии с первым законом Кирхгофа.
D:\ОТЦиС\Упражнения\Тема_6c\Пример_2
* Напомним, что конденсатор в стационарном состоянии эквивалентен разъёму.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.