Классический анализ переходных процессов в RС-цепях
первого порядка
Задача 6.8
|
Рис. 6.1 |
Запишите выражение и постройте график тока iо(t) источника напряжения uо(t) после замыкания ключа в цепи Рис. 6.1, если R1 = 2
кОм, C2 = 2 мкФ, R3 = 1 кОм, C4 = 1 мкФ, а |
Решение.
Особенность рассматриваемой задачи состоит в том, что схема цепи после коммутации содержит два конденсатора C2 и C4. Однако, в схеме цепи, освобождённой от источника напряжения, они включены параллельно и могут быть заменены одним эквивалентным конденсатором ёмкостью C2 + C4. Такая схема описывается однородным дифференциальным уравнением первого порядка. Поэтому цепь после коммутации является цепью первого порядка.
Сначала решим эту задачу аналитически.
Совместим момент коммутации в цепи Рис. 6.1 с началом отсчёта относительного времени t в ней, то есть с моментом времени t = 0, когда
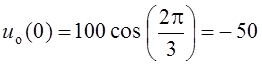 В,
В, 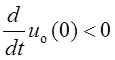 .
.
|
Рис. 6.2 |
По умолчанию эта цепь до коммутации (Рис. 6.2) находится в стационарном состоянии, в котором напряжения u2(t) и u4(t) конденсаторов С2 и С4 при t < 0 равны нулю. Следовательно, начальные (то есть накануне коммутации) значения напряжений конденсаторов также равны нулю:
u2(0–) = 0, u4(0–) = 0.
В качестве переменной состояния (независимой переменной) цепи после замыкания ключа (при t ³ 0) выберем напряжение одного из двух конденсаторов, например, напряжение u2(t) конденсатора С2. В этом случае напряжение u4(t) конденсатора C4 станет зависимой переменной цепи, являющейся линейной функцией переменной состояния u2(t) (и задающего напряжения uo(t))
u4(t) = uo(t) – u2(t).
|
|
|
|
Рис. 6.3 |
Рис. 6.4 |
Составим затем уравнение состояния цепи после коммутации, в котором искомой функцией будет переменная состояния цепи – напряжение u2(t) конденсатора C2. Считая известным выражение его мгновенного значения и опираясь на принцип компенсации *, изобразим схему замещения цепи для произвольного момента времени t ³ 0. Для схемы цепи Рис. 6.3 в результате такой замены получим схему замещения, как на Рис. 6.4. Из неё находим выражение тока i2(t) конденсатора C2:
i2 = – i1 + i3 + i4
или, поскольку u1(t) = u2(t),
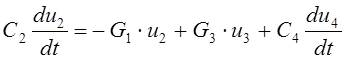 .
.
Интегрируя это выражение в пределах от 0– до 0+, получаем соотношение между начальными u2(0–), u4(0–) и стартовыми u2(0+), u4(0+) значениями напряжений конденсаторов
![]() .
.
С учётом связи стартовых значений напряжений конденсаторов
u4(0+) = uo(0) – u2(0+)
находим
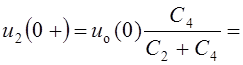
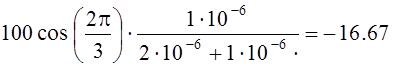 В.
В.
Вернёмся к последнему выражению тока конденсатора C2, из которого, после несложных преобразований, учитывая линейное соотношение
u4(t) = uo(t) – u4(t),
справедливое при t ³ 0, получаем искомое уравнение состояния цепи, записанное в нормальной форме (форме Коши):
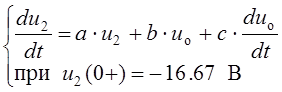
Здесь
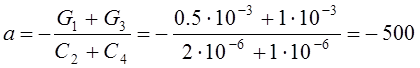 с-1;
с-1;
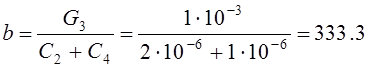 с-1;
с-1;
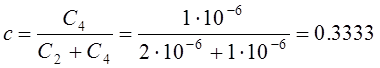 .
.
Далее, как обычно, задачу решаем в два этапа. Сначала получим выражение переменной состояния цепи u2(t) при t ³ 0 – напряжения конденсатора C2 после замыкания ключа, а затем для тех же моментов времени t найдём выражение искомой зависимой переменной – тока iо(t) источника напряжения uо(t) цепи Рис. 6.3.
I этап. При t ³ 0 напряжение конденсатора C2 представим суммой двух составляющих
![]() ,
,
где
![]() – принуждённая составляющая
напряжения конденсатора C2, совпадающая с его гармонической составляющей;
– принуждённая составляющая
напряжения конденсатора C2, совпадающая с его гармонической составляющей;
![]() – свободная составляющая напряжения
конденсатора.
– свободная составляющая напряжения
конденсатора.
|
Рис. 6.5 |
Из комплексной схемы цепи после коммутации (Рис. 6.5) находим сначала комплексную амплитуду Um2 принуждённой составляющей напряжения конденсатора u2пр(t):
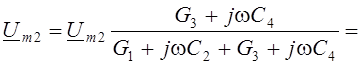
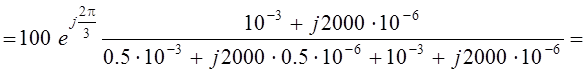
![]() В.
В.
Вычислим попутно выражение значение комплексной амплитуды Imo принуждённой составляющей тока ioпр(t) источника напряжения uо(t):
![]()
![]() А.
А.
Запишем далее выражения принуждённых составляющих переменной состояния цепи u2(t) и искомого тока io(t) источника напряжения (t ³ 0)
![]() В
В
![]() А.
А.
Для составления выражения свободной составляющей составляющих переменной состояния цепи получим сначала характеристическое уравнение и найдём его корни. Обращаясь к уравнению состояния цепи, записываем его характеристическое уравнение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.