![]() ,
,
единственный корень которого равен
![]() с-1.
с-1.
Найдём попутно значение постоянной времени t рассматриваемой цепи
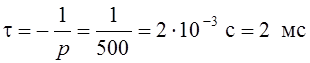 .
.
При единственном корне характеристического уравнения
![]() .
.
В соответствии с принятым представлением при t ³ 0 напряжение конденсатора
![]() .
.
Полагая здесь t = 0+, находим
![]() В.
В.
Следовательно, напряжение конденсатора u2(t) в заданной цепи представляется выражением:
![]()
![]() .
.
Здесь s(t) – единичная ступенчатая функция (функция Хевисайда).
II этап. Выражение искомого тока io(t) источника напряжения uо(t) в цепи Рис. 6.3 получим сложением токов i1(t) резистора R1 и i2(t) конденсатора С2:
![]() ,
,
где
![]() мА,
мА,
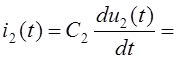
![]()
![]() мА.
мА.
Здесь d(t) = s¢(t) – единичная импульсная функция (функция Дирака) *.
Складывая полученные выражения токов i1(t) и i2(t), а также используя полученное ранее выражение гармонической составляющей тока io(t) источника напряжения, после приведения подобных получим
![]() мА.
мА.
Обратите внимание на бесконечно короткую импульсную составляющую тока io(t) источника напряжения – [ – 33.33×10– 3 d(t) мА], под воздействием которой напряжения u2(t) и u4(t) конденсаторов C2 и C4 мгновенно изменяют свои значений от нулевых начальных до ненулевых стартовых значений. Действительно, поскольку
![]() А,
А,
то стартовые значения напряжений конденсаторов равны соответственно
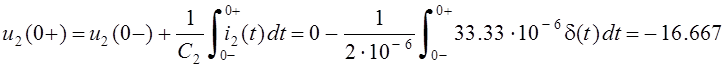 В;
В;
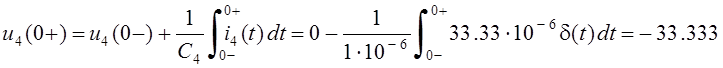 В.
В.
Проверка:
![]() В.
В.
Аналитическое решение рассматриваемой задачи завершено. Остаётся составить таблицу конечных значений функции io(t) и построить её график, например, на интервале [0, 3…5t].
Численное решение этой задачи осуществляется также в рассмотренные два этапа.
Обратимся сначала к полученному ранее уравнению для переменной состояния цепи u2(t) в виде
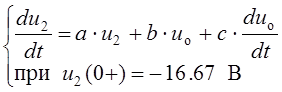 ,
,
в котором
a = – 500 с-1, b = 333.3 с-1, c = 0.3333.
Численное решение этого уравнения при 0 £ t£ 5 мс найдём с помощью функции rkfixed математического пакета MathCad 7 Pro, реализующей метод Рунге-Кутта с фиксированным шагом. Для этого задаём последовательно:
![]() –
стартовое значение переменной состояния цепи u2(0+);
–
стартовое значение переменной состояния цепи u2(0+);
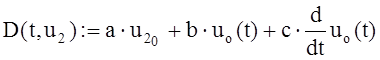 – выражение её первой
производной;
– выражение её первой
производной;
![]() –
вычисление значений переменной состояния цепи u2(t) в пятистах точках (500) интервала времени [0,0.005] с;
–
вычисление значений переменной состояния цепи u2(t) в пятистах точках (500) интервала времени [0,0.005] с;
![]() –
номера точек разбиения интервала времени пробегают значения от 0 до числа строк
без 1 матрицы Z.
–
номера точек разбиения интервала времени пробегают значения от 0 до числа строк
без 1 матрицы Z.
![]() –
элементам вектора t присваивают значения
элементов первого столбца матрицы Z.
–
элементам вектора t присваивают значения
элементов первого столбца матрицы Z.
![]() –
элементам вектора u2
присваивают значения элементов второго
столбца матрицы Z.
–
элементам вектора u2
присваивают значения элементов второго
столбца матрицы Z.
Искомая зависимая переменная io(t) определяется суммой
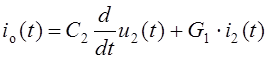 .
.
Для аппроксимации на интервале [0,0.005
с] вектор-функции ![]() дискретного
аргумента
дискретного
аргумента ![]() функцией
u2(x) непрерывной переменной x (относительного времени)
воспользуемся функцией кусочно-линейной интерполяции linterp(VX,VY,x) математического пакета MathCad 7 Pro:
функцией
u2(x) непрерывной переменной x (относительного времени)
воспользуемся функцией кусочно-линейной интерполяции linterp(VX,VY,x) математического пакета MathCad 7 Pro:
![]()
Теперь можно записать выражение зависимой переменной io(t) в протоколе MathCad 7 Pro:
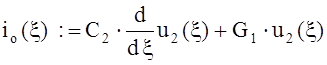 .
.
|
(Рис. 6.6) |
Потерянная при численном анализе бесконечно короткая импульсная составляющая тока io(t) источника напряжения Idod(t) может быть легко восстановлена путём предельного перехода в операторном выражении Io(s) этого тока (Рис. 6.6):
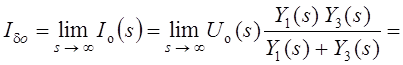
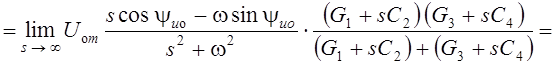
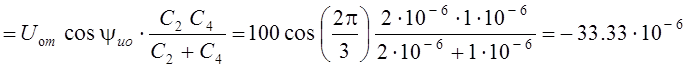 Ас.
Ас.
Рекомендуется самостоятельно составить таблицу конечных значений функции io(t) и построить её график на том же интервале [0, 3…5t]. Сравните и проанализируйте результаты аналитического и численного анализа переходного процесса в цепи. C:\ОТЦиС\Упражнения\Тема_6b\Примеры_6b\Пример 8
* Любой элемент с известным значением напряжения может быть эквивалентно заменён источником напряжения известного значения.
* Если
y(t) = x(t)×s(t),
то по правилам дифференцирования произведения функций находим
y¢(t) = x¢(t)×s(t) + x(0)×d(t).
Здесь написано x(0), так как d(t) = 0 при t ¹ 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.