Расчет системы автоматического регулирования скорости вращения вала двигателя постоянного тока с независимым возбуждением (n=2500 об/мин; Рном=0,76 кВт), страница 9

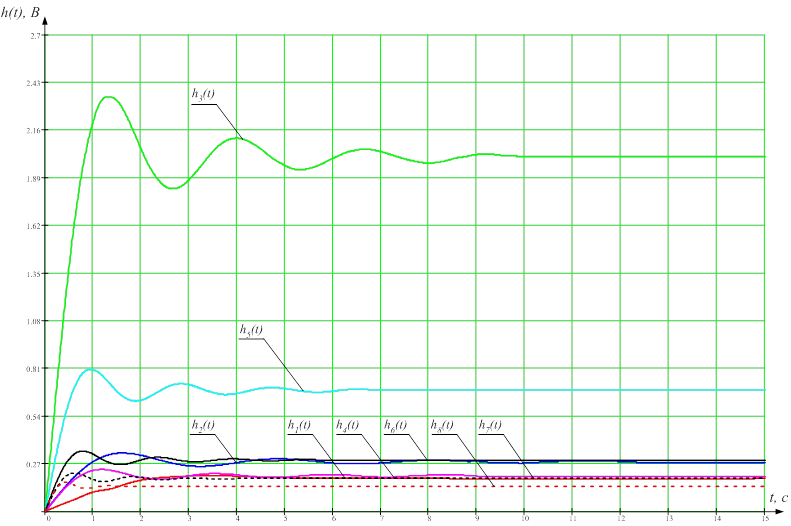
Рисунок 4 — Переходные процессы, построенные по трапециям

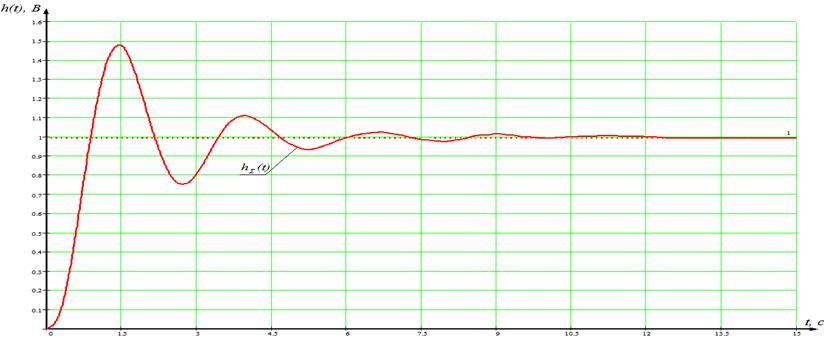Рисунок 5 — Суммарный переходной процесс

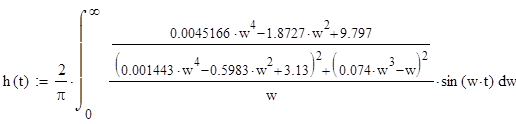
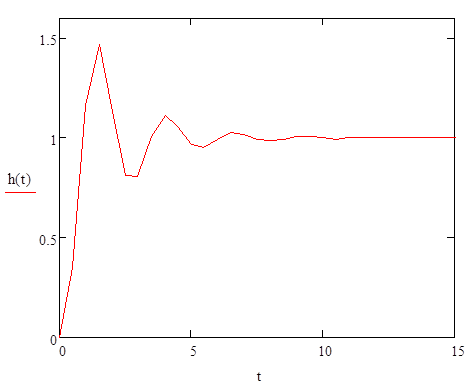
Рисунок 6 — Переходной процесс, построенный в MathCad

Рисунок 7 — Переходной процесс, построенный в VisSim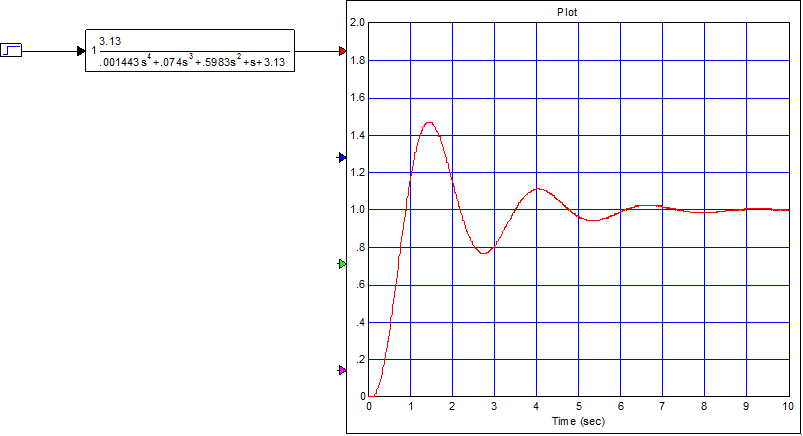

1.5 Анализ качества переходного процесса

По известному переходному процессу можно определить прямые показатели качества:

Вид переходного процесса – колебательный с затухающими колебаниями, следовательно, система работоспособна;

Установившееся значение (статическое отклонение):

 (В);

Максимальное отклонение регулируемой величины или динамическое отклонение:

, (В);

Статическая ошибка (так как система астатическая, то):

;

Время нарастания:

 (с);

Время достижения первого максимума:

 (с);

Время переходного процесса (время регулирования):

 (с);

Перерегулирование:

;

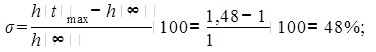Данное значение превышает диапазон σ ≤ 30 – 40%, следовательно, качество регулирования – неудовлетворительное;

Степень затухания (определяется только для колебательных систем):

;

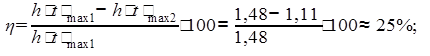Так как степень затухания не входит в диапазон η ≥ 70 – 80%, то это не удовлетворяет условиям;

Логарифмический декремент затухания q:

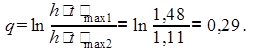
2 Синтез АСР

Задачей синтеза является определение вида и структуры корректирующего

устройства, а так же расчет его параметров. Для решения нашей задачи используем синтез методом ЛАЧХ. Данный метод основан на соответствии между логарифмическими частотными характеристиками разомкнутой системы и ее статическими и динамическими свойствами в замкнутом состоянии. 

2.1 Построение логарифмической амплитудно-частотной характеристики некорректированной системы

Так как генератор, двигатель, тахогенератор и исполнительный двигатель включены последовательно, то логарифмическая амплитудно-частотная характеристика разомкнутой некорректированной системы находится как сумма четырех характеристик:

L_нк(w)=L_г(w)+L_дв(w)+L_тг(w)+L_ид(w).

2.1.1 Построение логарифмической амплитудно-частотной характеристики генератора

Генератор представляет собой инерционное звено первого порядка. Параметры логарифмической амплитудно-частотной характеристики определяются из передаточной функции:

Частота сопряжения:

 (Гц),

Амплитуда:

 (дБ).

Асимптотическая логарифмическая амплитудно-частотная характеристика представлена на рисунке 8.

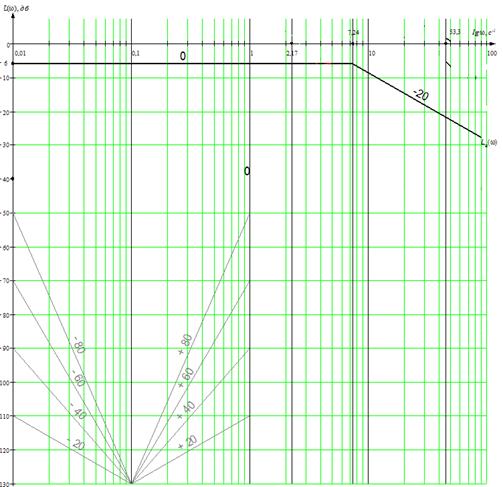
Рисунок 8 — ЛАЧХ генератора

2.1.2 Построение логарифмической амплитудно-частотной характеристики двигателя

Для построения логарифмической амплитудно-частотной характеристики двигателя необходимо проверить выполнения условия:

4Т_я>Т_эм.

По данным передаточной функций двигателя

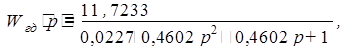
получается

Следовательно, данная передаточная функция является инерционным звеном второго порядка, передаточная функция которого выглядит следующим образом:

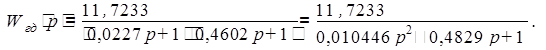
Частота сопряжения большая:

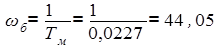 (Гц).

Частота сопряжения меньшая:

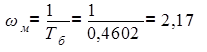 (Гц).

Амплитуда:

 (дБ).

Асимптотическая логарифмическая амплитудно-частотная характеристика показана на рисунке 9.

2.1.3 Построение логарифмической амплитудно-частотной характеристики тахогенератора

Тахогенератор представляет собой пропорциональное звено.

Передаточная функция тахогенератора:

Амплитуда:

 (дБ).

Логарифмическая амплитудно-частотная характеристика тахогенератора представлена на рисунке 10 и обозначена L_т(ω).

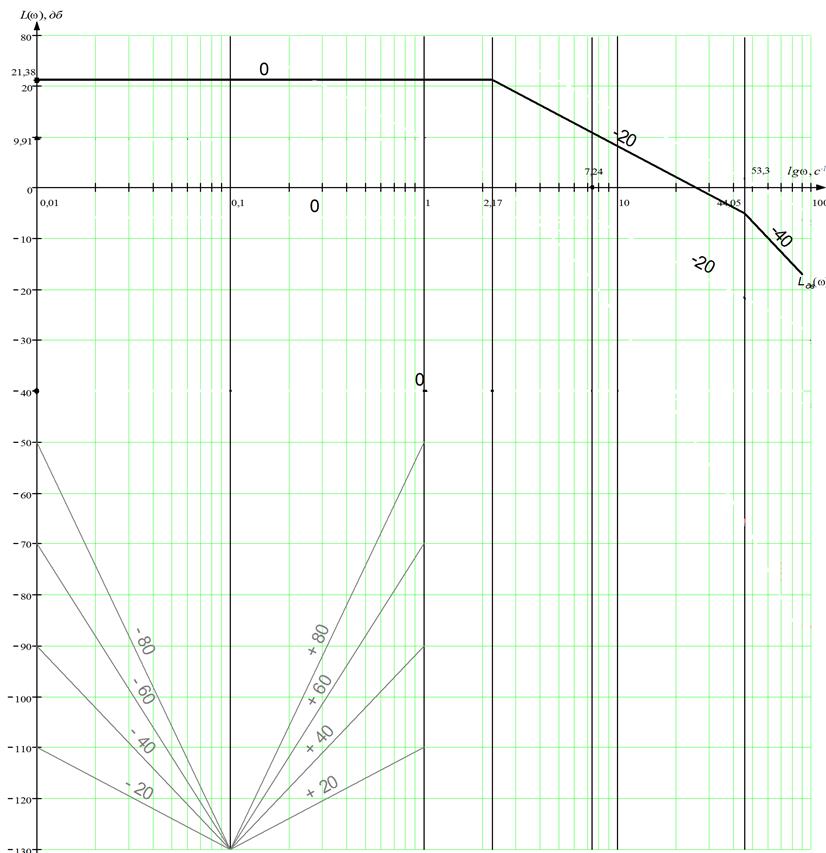Рисунок 9 — ЛАЧХ двигателя

2.1.4 Построение логарифмической амплитудно-частотной характеристики исполнительного двигателя

Исполнительный двигатель (в комплекте с редуктором) представляет собой интегрирующее звено, с передаточной функцией:

          Логарифмическая амплитудно-частотная характеристика интегрирующего звена представляет собой прямую линию, проведенную через точку ω = 1Гц и L(ω) = 20 lg К = 20 lg 53,3 = 34,53 (дБ). Ось частот логарифмическая амплитудно-частотная характеристика пересекает при значении ω = К.

Логарифмическая амплитудно-частотная характеристика исполнительного двигателя представлена на рисунке 10 и обозначена L_ид(ω).

Логарифмическая амплитудно-частотная характристика разомкнутой некорректированной системы строим на рисунке 10 как сумму характеристик генератора, двигателя, тахогенератора и исполнительного двигателя, т. к. они включены последовательно.

2.2 Построение желаемой логарифмической амплитудно-частотной характеристики

При построении желаемой ЛАЧХ необходимо помнить, что исследуемая система должна быть минимально-фазовой.

Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, которая имеет желаемые, требуемые статические и динамические свойства.