Желаемая логарифмическая амплитудно-частотная характеристика состоит из трех участков: низких, средних и высоких частот.
Для построения участка низких частот необходим коэффициент системы, который из передаточной функции:
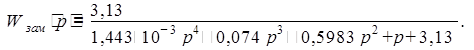
равен Кc = 3,13 (В).
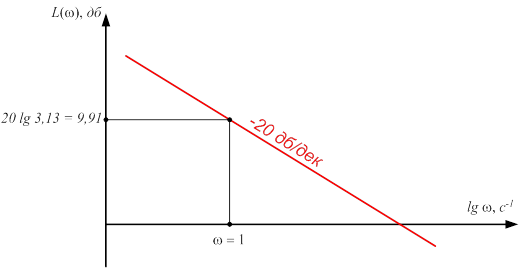
Рисунок 11 — Желаемая логарифмическая амплитудно-частотная характеристика на участке низких частот
Так как данная система является астатической, содержащей одно интегрирующее звено (порядок астатизма ν = 1), то логарифмическая амплитудно-частотная характеристика на участке низких частот представляет собой линию с наклоном –20 дБ/дек, проходящую через точку ω = 1Гц и L(ω) = 20 lg Кс.
Вид желаемой логарифмической амплитудно-частотной характеристики на участке низких частот представлен на рисунке 11.
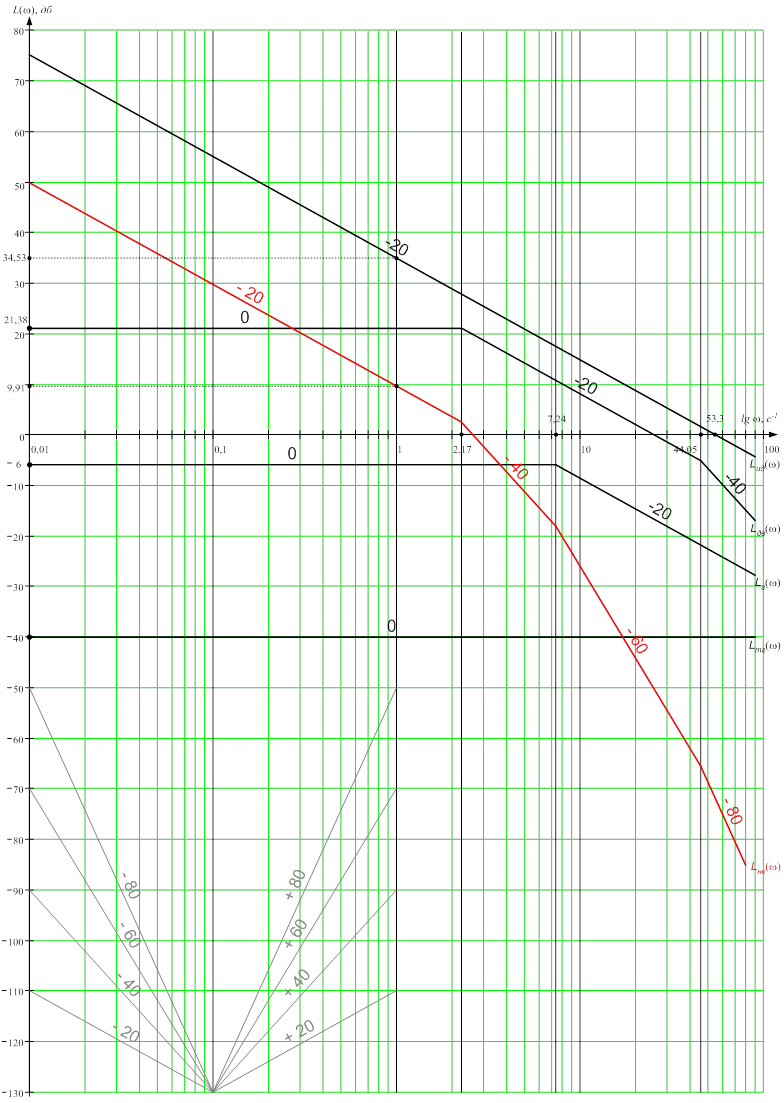
Рисунок 10 — логарифмические амплитудно-частотные характеристики элементов и неккоректированной системы
Логарифмическая амплитудно-частотная характеристика на участке средних частот представляет собой прямую с наклоном –20 дБ/дек, проходящую через частоту среза.
Кроме того, этот участок ограничен запасом устойчивости по амплитуде ΔL, который определяется из справочника [3] по круговым диаграммам в логарифмическом масштабе.
Частота среза определяется по номограмме [3] при перерегулировании σ = 25%:
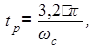
тогда при заданном времени регулирования tp = 1,5 частота среза будет равна:
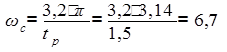(с).
По этой же номограмме определяется Рmax ≈ 1,2.
Тогда
По данным значениям Рmin и Рmax по круговым диаграммам определяем значение запаса устойчивости по амплитуде ±Δ равное ±15 дБ.
Участок средних частот представлен на рисунке 12.
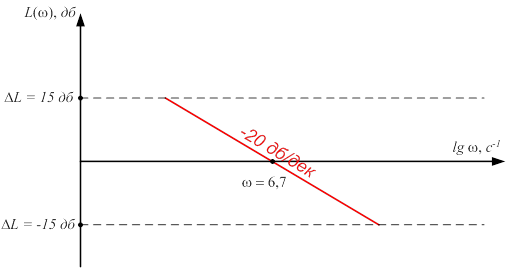
Рисунок 12 – Желаемая логарифмическая амплитудно-частотная характеристика на участке средних частот
Участок высоких частот не корректируют, желаемая логарифмическая амплитудно-частотная характеристика на этом участке идет либо параллельно логарифмической амплитудно-частотной характеристики некорректированной системы, либо совпадает с ней.
Участки низких и средних, а также средних и высоких частот сопрягают стандартными наклонами –60 и –80 дБ/дек.
Так как в данном случае сопряжение участков низких и средних частот выполнить невозможно, то чтобы система не потеряла своей устойчивости, поднимем желаемую логарифмическую амплитудно-частотную характеристику на участке низких частот параллельно самой себе вверх до совпадения линий низких и средних частот.
Новая получившаяся точка желаемой логарифмической амплитудно-частотной характеристики равна ω = 1Гц и L(ω) = 20 lg Кс.нов. Через эту точку будет проходить новая желаемая логарифмическая амплитудно-частотная характеристика (рисунок 13).
Для этого переноса необходимо увеличить коэффициент усиления системы. Новый коэффициент усиления системы будет равен :
20 lg Кc.нов = 16,73 (дБ),
тогда Кc.нов = 1016,73/20 = 6,863.
Получившийся коэффициент усиления оказался меньше критического коэффициента, следовательно, система не потеряла своей устойчивости, сократился лишь запас устойчивости с 60% до 12,3%.
Желаемая логарифмическая амплитудно-частотная характеристика представлена на рисунке 13 и обозначена Lж(ω).
2.3 Нахождение корректирующего устройства
Логарифмическая амплитудно-частотная характеристика корректирующего устройства находится графическим вычитанием логарифмической амплитудно-частотной характеристики некорректированной системы от желаемой:
Полученную характеристику можно реализовать последовательным соединением двух корректирующих устройств. В результате:
Wку(p)=W1(p)·W2(p)
или
Lку(p)=L1(w)+L2(w).
Результат вычитания приведен на рисунке 13. Полученную характеристику можно реализовать двумя корректирующими элементами с логарифмическими амплитудно-частотными характеристиками, изображенными на рисунке 14.
Логарифмические амплитудно-частотные характеристики L1(w) и L2(w) показаны на рисунке 15.
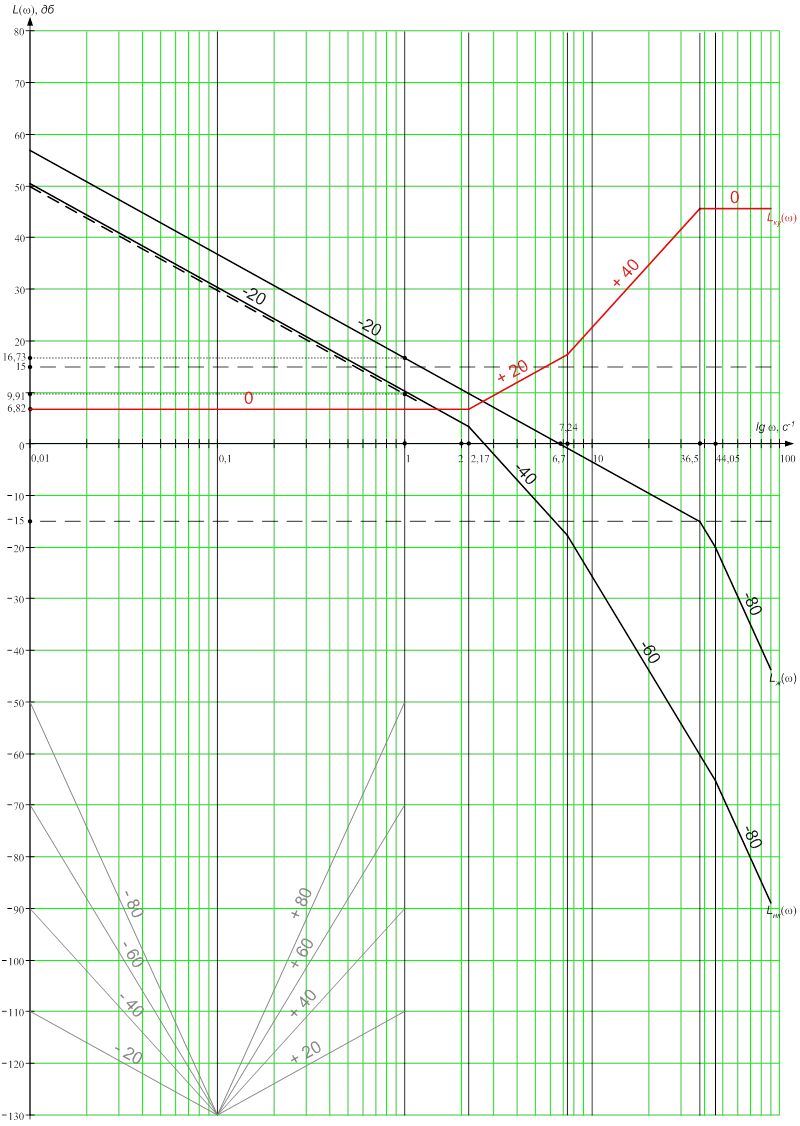
Рисунок 13 — Логарифмическая амплитудно-частотная характеристика желаемая и корректирующего устройства
2.3.1 Первое корректирующее устройство
Из справочника [3] выбираем:
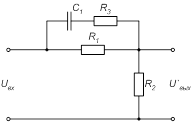
Рисунок 14 – Электрическая схема первого корректирующего устройства
Для нахождения передаточной функции корректирующего устройства рассчитаем его параметры. Из рисунка 15 следует, что:
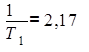
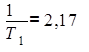(с–1); 
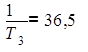(с–1);
откуда можно найти постоянные времени:
(с); 
(с).
Рассчитаем коэффициент передаточной функции:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.