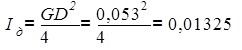Расчет системы автоматического регулирования скорости вращения вала двигателя постоянного тока с независимым возбуждением (n=2500 об/мин; Рном=0,76 кВт), страница 3

 (кг×м).

Далее определяем постоянные двигателя:

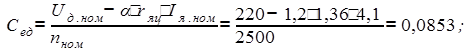
 (Н×м/А).

По приближенной формуле определяем индуктивность якоря L_яд:

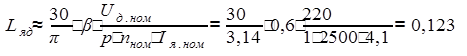 (Гн),

где b=0,25¸0,6 (нижнее значение принимается для компенсированных машин, верхнее – для некомпенсированных). Принимаем b=0,6, т.к. у двигателей серии МИ нет компенсационных обмоток.

Момент инерции на валу двигателя:

(кг∙м²).

Подставив численные значения найденных параметров в коэффициенты передаточной функции двигателя, получим:

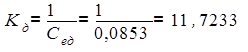 (об/мин×В),

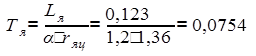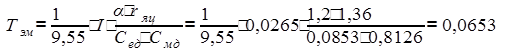 (с),

 (с),

Генератор включен последовательно с двигателем, поэтому передаточная функция генератора с двигателем имеет вид:

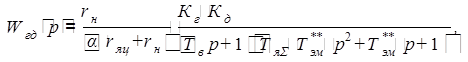
где 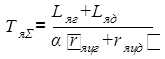     – суммарная постоянная времени цепи якоря генератора и двигателя, с;

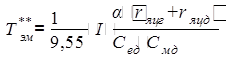 – электромеханическая постоянная времени двигателя при работе от генератора, с.

 (с),

 (с).

Передаточная функция генератора с двигателем:

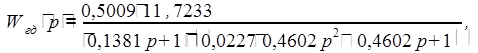
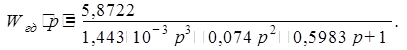
1.1.3. Выбор и расчет тахогенератора

          Тахогенераторами  называются небольшие электрические машины, предназначенные для преобразования механического перемещения вращения вала в электрический сигнал  ̶ выходное напряжение. Тахогенераторы в схемах автоматики используются для измерения скорости вращения.

          Тахогенератор выбираем таким образом, чтобы при заданной скорости вращения вала двигателя находиться на линейном участке его выходной характеристики. Характеристики тахогенератора ТГ-4 приведены таблице 3.

Таблица 3 – Характеристики тахогенератора ТГ-4

Напряжение возбуждения, В	Частота сети, ГЦ	Крутизна генераторной ЭДС, мВ/об/мин	Остаточное напряжением (не более), мВ	Полное выходное сопротивление генераторной обмотки
110	400	10	-	-

Окончание таблицы 3

Ток в обмотке возбуждения, А	Мощность возбуждения, Вт	Номинатльная скорость вращения, об/мин	Статический момент трения (не более),кг×м	Вес, кг
0,3	12	6000	15×10-5	1,5

Передаточная функция тахогенератора:

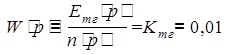 (В/об/мин).

1.2 Нахождение передаточных функций разомкнутой и замкнутой системы

Структурная схема системы представлена на рисунке 2.

Рисунок 2 — Структурная схема АСР

Со структурной схемы видно, что элементы соединены последовательно, поэтому передаточная функция разомкнутой системы будет состоять из перемноженных передаточных функций всех элементов:

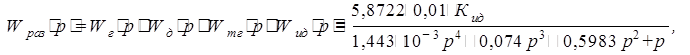
где К_ид – коэффициент передачи исполнительного двигателя, определяемый из условий устойчивости.

Тогда замкнутую передаточную функцию системы найдем следующим образом:

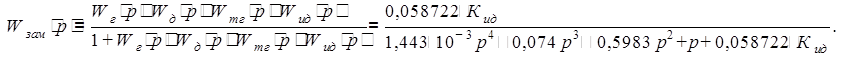
1.3 Анализ устойчивости АСР

Выпишем характеристическое уравнение (знаменатель передаточной функции замкнутой системы) и исследуем систему на устойчивость. Устойчивость АСР определим по критерию Гурвица.

Отсюда следует, что коэффициенты равны:

а₀ = 1,443∙10^–3; а₁ = 0,074; а₂ = 0,5983; а₃ = 1; а₄ = 0,0587∙К_ид.

Определитель Гурвица для системы четвертого порядка будет иметь вид:

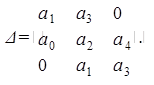
Определим коэффициент передачи исполнительного двигателя К_ид. Приравняем определитель к нулю, решим это уравнение, найдем К_ид.

Для определения коэффициента передачи исполнительного двигателя приравняем определитель к нулю и решим это уравнение относительно К_ид:

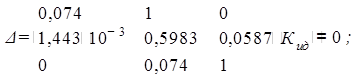
Этот же коэффициент является и критическим коэффициентом К_кр.

Для удовлетворительного качества процесса регулирования выбираем К_ид с 60% запасом устойчивости, т.е.:

             

             

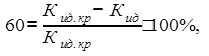
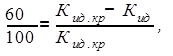
Проверим правильность нахождения коэффициента, решив главный определитель Гурвица и его диагональные миноры с новыми параметрами. Итак, для системы четвертого порядка получаем:

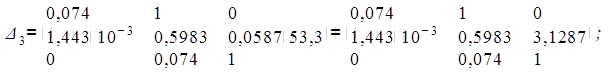
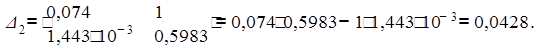
Так как главный определитель Гурвица и все его диагональные миноры больше нуля, то система устойчива.

Окончательно передаточные функции разомкнутой и замкнутой системы выглядит следующим образом:

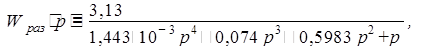
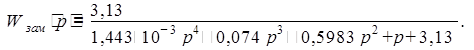
1.4 Построение переходного процесса по вещественной частотной характеристике замкнутой системы

Для построения вещественной частотной характеристики подставляем в передаточную функцию замкнутой системы p = jw: