Расчет системы автоматического регулирования скорости вращения вала двигателя постоянного тока с независимым возбуждением (n=2500 об/мин; Рном=0,76 кВт), страница 4

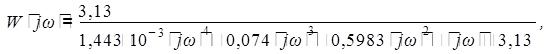
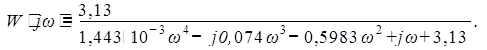
Избавимся от комплексных составляющих знаменателя путем домножения числителя и знаменателя на комплексно-сопряженное выражение знаменателю.

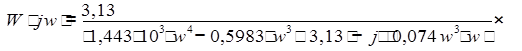
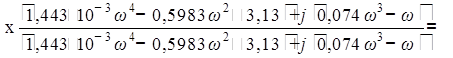
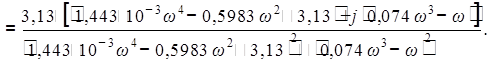
Из полученного выражения выделим вещественную часть и получим:

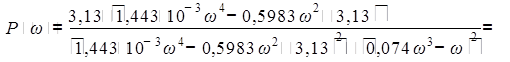
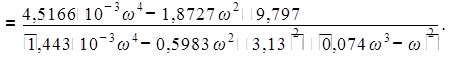
Изменяя частоту от нуля до бесконечности, найдем значения вещественной частотной характеристики. Данные сведем в таблицу 4.

Таблица 4 — Данные для построение ВЧХ

Продолжение таблицы 4

По данным таблицы 4 построим вещественную частотную характеристике, которую разобьем на трапеции (рисунок 3).

Определим параметры трапеций по графику и сведем их в таблицу 5.

Таблица 5 — Параметры трапеций

Коэффициент наклона рассчитываем по формуле:

χ=ω_d/ω_с.

          где     ω_с – частота среза (большая сторона трапеции),

ω_d – динамическая частота (меньшая сторона трапеции).

Для проверки правильности разбивки ВЧХ воспользуемся формулой:

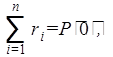
где ri – высота i-ой трапеции; Р(0) – значение Р(ω) при ω = 0.

Согласно разбивке на трапеции следует, что:

Исходя из графика, изображенного на рисунке 2, получаем Р(0)= 1, а сумма высот трапеций равна:

– 0,185 + 0,280 + 2,005 + 0,200 – 0,685 – 0,290 – 0,185 – 0,140 = 1, что соответствует действительности. Далее составим таблицы для каждой трапеции в отдельности. Переход от к производиться по формуле:

,

где r – высота трапеции;

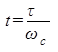– реальное время;

–  табличное время.

Таблицы с данными по трапециям приведены в таблицах 6 — 13. Затем построим суммарную переходную характеристику (рисунок 5) и процесс, построенный на интегральной зависимости от вещественной части комплексной передаточной функции, с помощью MathCad (рисунок 6).

,

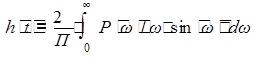где h(t) — переходная характеристика;

P(ω) – вещественная часть комплексной передаточной функции. 

Также затем построим переходной процесс с помощью VisSim (рисунок 7).

 Таблица 6 —  Данные для построения 1 трапеции         Таблица 7 Данные для построения 2 трапеции