![]() ,
,
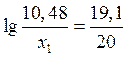 ,
,
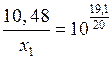
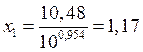
![]() ,
,
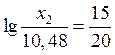 ,
,
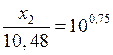
![]()
5.2.3 Построение участка высоких частот
Этот участок не оказывает большого влияния на качество процесса регулирования. Данный участок строится параллельно ЛАЧХ некорректированного звена или полностью с ней совпадает.
5.3 Графическое построение желаемой ЛАЧХ ![]() и ЛАЧХ корректирующего устройства
и ЛАЧХ корректирующего устройства![]()
Построение ЛАЧХ корректирующего устройства выполняем графически на основе выражения:
![]()
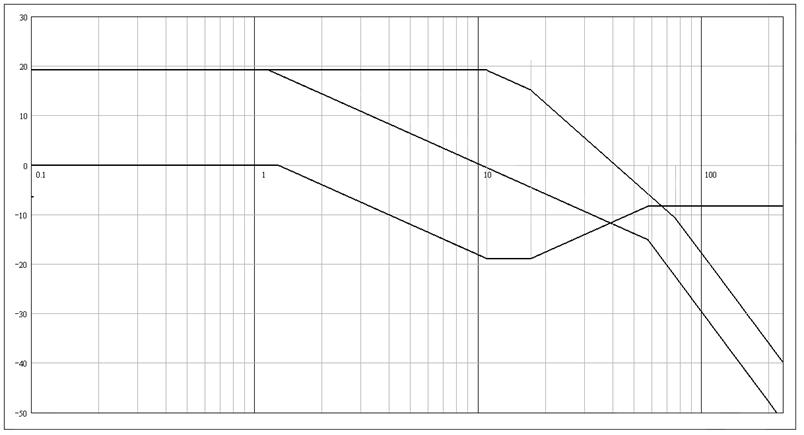
Рисунок 10 − Построение ЛАЧХ желаемой системы ![]() и корректирующего
устройства
и корректирующего
устройства ![]()
6 Выбор схемы корректирующего устройства
Пользуясь схемами корректирующих звеньев приведенных в [метод. указание приложение 3], произведем выбор схемы корректирующего устройства пользуясь его ЛАЧХ.
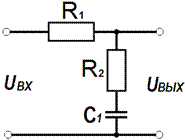
Рисунок 11 − Схема первого корректирующего звена
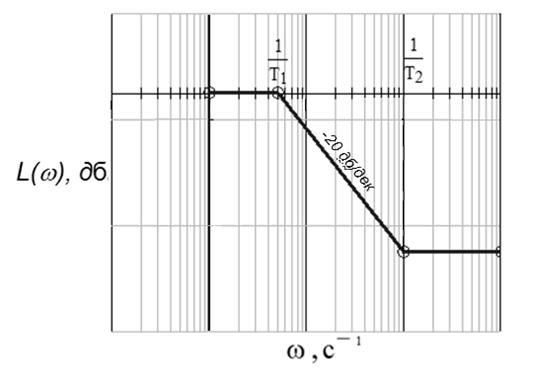
Рисунок 12 − ЛАЧХ первого корректирующего звена
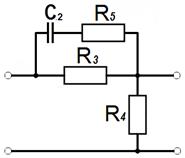
Рисунок 13 − Схема второго корректирующего звена
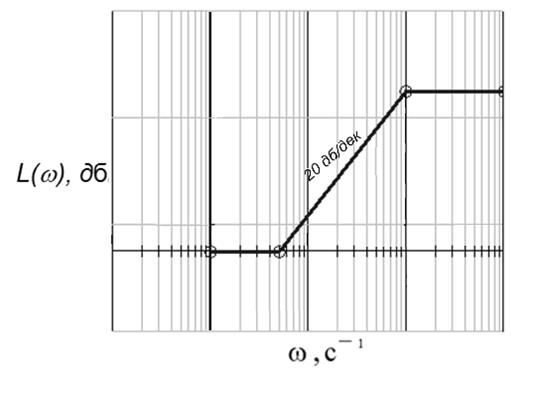
Рисунок 14 − ЛАЧХ второго корректирующего звена
6.1 Расчет элементов схемы первого корректирующего звена
Передаточная функция первого корректирующего звена имеет вид:
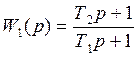 ,
,
где ![]() и
и
![]() находим из
выражения:
находим из
выражения:
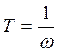 .
.
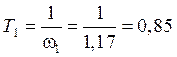 с;
с;
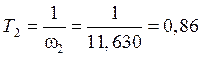 с.
с.
Для
расчета примем ![]() мкФ.
мкФ.
Выразим
![]() из
выражения:
из
выражения:
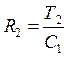 ;
;
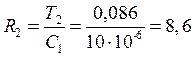 кОм.
кОм.
Вычислим
![]() из
выражения:
из
выражения:
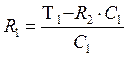 ;
;
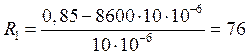 кОм.
кОм.
Запишем передаточную функцию первого корректирующего звена с числовыми значениями:
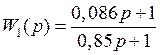 .
.
6.2 Расчет элементов схемы второго корректирующего звена
Передаточная функция второго корректирующего звена:
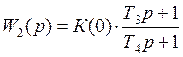 .
.
Определим
значения ![]() и
и ![]() :
:
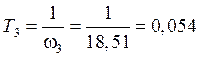 с;
с;
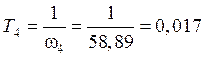 с;
с;
Для
расчета примем ![]() мкФ,
мкФ, ![]() кОм.
кОм.
Найдем
![]() из
выражения:
из
выражения:
![]()
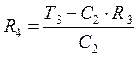 ;
;
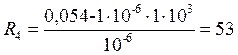 кОм.
кОм.
Выразим
![]() из выражения:
из выражения:
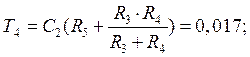
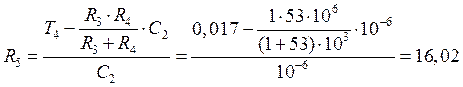 кОм.
кОм.
Определим
![]() :
:
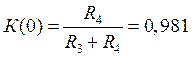
Учитывая, что передаточные функции второго и третьего корректирующего звена равны, то их общая передаточная функция с числовыми значениями будет иметь вид:
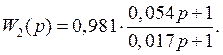
6.3 Расчет усилителя
Для расчета коэффициента усиления воспользуемся формулой:
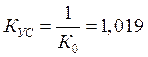
6.4 Построение ЛАЧХ корректирующего устройства
Графическое построение производим по формуле:
![]()
![]() на графике не отображено,
на графике не отображено, ![]() компенсируется
компенсируется ![]()
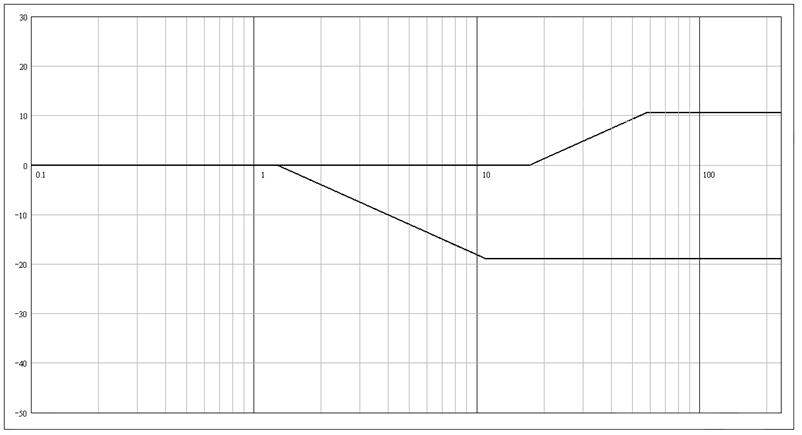
Рисунок 15 − ЛАЧХ корректирующих звеньев
Окончательно передаточная функция корректирующего устройства примет вид:
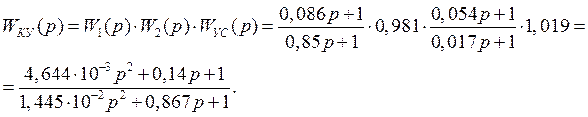
Полученные значения сопротивлений и емкостей округлим по стандартному ряду.
Для первого корректирующего звена:
![]() мкФ;
мкФ;
![]() кОм;
кОм;
![]() кОм.
кОм.
Для второго корректирующего звена:
![]() мкФ;
мкФ;
![]() кОм;
кОм;
![]() кОм;
кОм;
![]() кОм.
кОм.
Усилителя:
![]()
6.5 Построение электрической схемы корректирующей цепи
Строим электрическую схему корректирующего устройства, путем соединения электрических схем используемых корректирующих звеньев и усилителя.
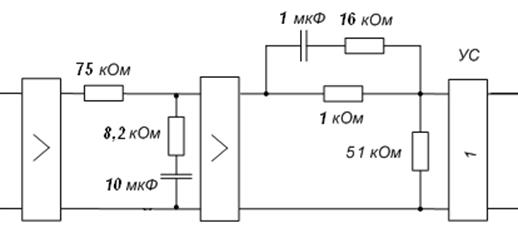
Рисунок 16 − Электрическая схема корректирующей цепи
7 Анализ устойчивости системы после коррекции
7.1 Составление передаточной функции скорректированной системы
Структурная схема скорректированной системы будет иметь вид:

Рисунок 17 − Структурная схема скорректированной системы
Так как наше корректирующее устройство последовательное, то передаточная функция скорректированной разомкнутой системы примет вид:
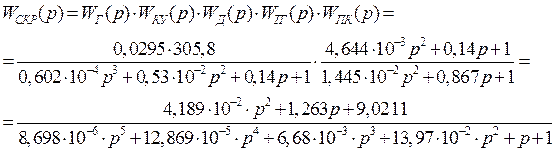
Далее находим передаточную функцию скорректированной замкнутой системы:
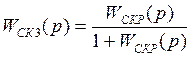 ;
;
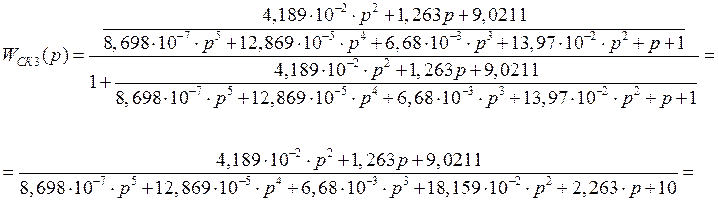
7.2 Определение устойчивости скорректированной системы
Проверим выполнение правила Стодолы для этого выпишем характеристическое уравнение:
![]() .
.
Правило Стодолы выполняется, т.е. все коэффициенты характеристического уравнения имеют один знак. Но так как наша скорректированная система шестого порядка, то правило Стодолы является необходимым, но недостаточным поэтому для определения устойчивости воспользуемся критерием устойчивости Гурвица.
Для этого по характеристическому уравнению замкнутой скорректированной системы составим главный определитель Гурвица и диагональные миноры:
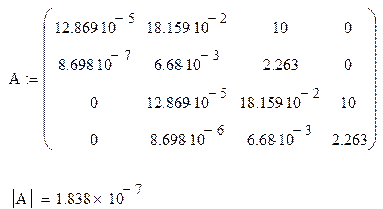
Анализ полученных результатов: Полученная скорректированная система в замкнутом состояние, является устойчивой, так как главный определитель Гурвица и все его диагональные миноры больше нуля. Следовательно мы можем построить переходной процесс и определить показатели качества.
7.3 Построение переходного процесса скорректированной системы
Для построения переходного процесса воспользуемся ПП VisSim.
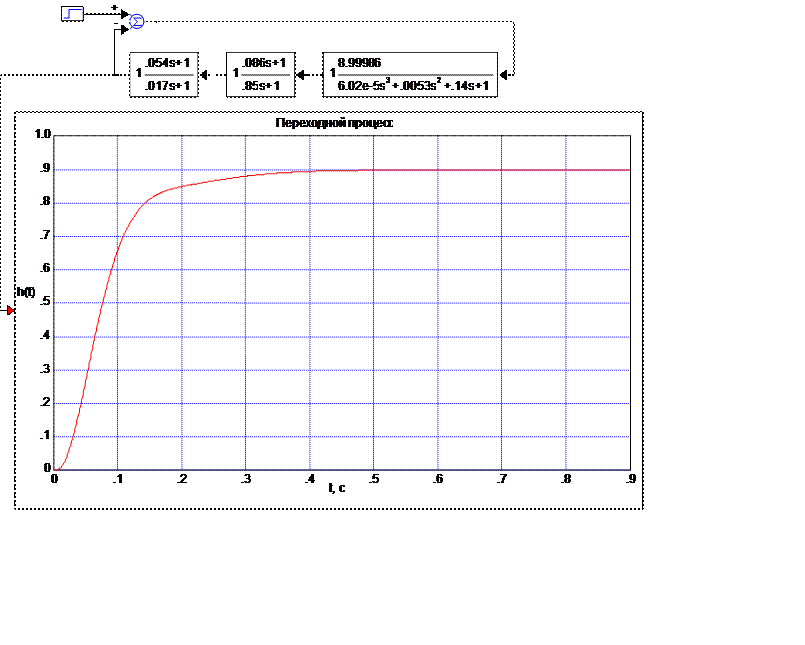
Рисунок 18 − Переходной процесс скорректированной системы
8 Анализ качества процесса регулирования скорректированной системы
Для анализа качества воспользуемся прямыми показателями качества.
1) Вид переходного процесса:
Монотонный без перерегулирования.
2) Установившееся значение регулируемой величины:
![]() .
.
3) Статическая ошибка:
![]() .
.
4) Время регулирования:
![]() с.
с.
Анализ полученных результатов: Полученные показатели
качества удовлетворяют заданным, время регулирования ![]() с,
без перерегулирования, следовательно в результате синтеза мы добились требуемых
показателей качества процесса регулирования.
с,
без перерегулирования, следовательно в результате синтеза мы добились требуемых
показателей качества процесса регулирования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.