Расчет системы автоматического регулирования скорости вращения вала двигателя постоянного тока с независимым возбуждением (n=1500 об/мин; Рном=6 кВт), страница 4

Вычисляем приближенно величину индуктивности якоря L_ЯД определяют  по формуле 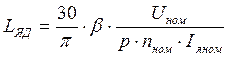2.

,                                                (2)

где b=0,3, т.к. двигатели серии П имеют легкую компенсационную обмотку.

.

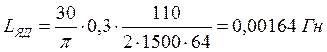Момент инерции на валу двигателя:

 

Подставив численные значения найденных параметров в коэффициенты передаточной функции двигателя, получим:

;

;

;

.

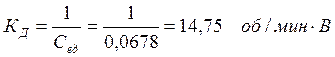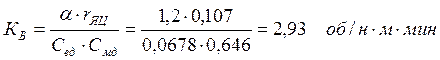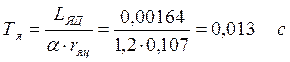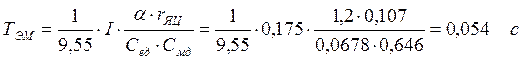Передаточная функция двигателя с рассчитанными коэффициентами имеет вид:

.

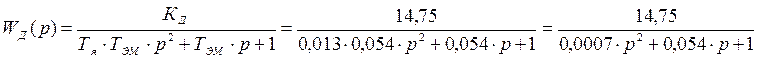2.2 Расчет передаточной функции генератора

Передаточная функция генератора имеет вид:

.

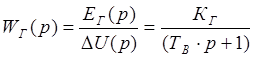Нагрузку считаем активной, индуктивностью обмотки якоря пренебрегаем. Начальный поток полагаем номинальным, внутреннее сопротивление источника возбуждения не учитываем. Находим конструктивную постоянную.

 ,

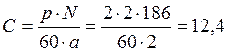где .

Откуда .

Номинальный поток возбуждения рассчитываем по формуле:

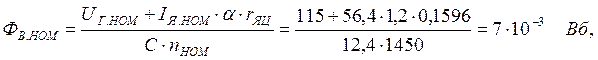
где a= 1,2 − коэффициент, учитывающий перегрев обмотки управления по сравнению с температурой 15⁰С.Определяем номинальный ток возбуждения и м.д.с. на полюс:

;

.

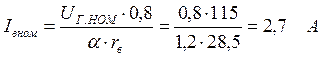По найденным значениям Ф_{в ном} и F_ном получаем масштабные коэффициенты по осям универсальной кривой намагничивания:

;           .

По кривой намагничивания при Ф_в=Ф_{в ном} находим :

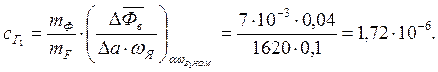
Принимаем σ_Г =1,2 – коэффициент, учитывающий рассеяние магнитного потока генератора ,определим индуктивность цепи возбуждения L_B:

.

Находим постоянную времени генератора:

.

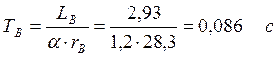Коэффициент передачи генератора:

.

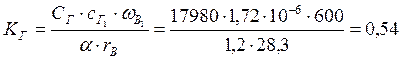Передаточная функция генератора с учетом нагрузки имеет вид:

 

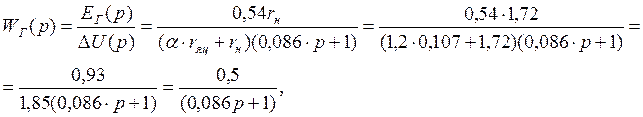
где сопротивление нагрузки двигателя,

 Ом.

Определим коэффициент нагрузки:

.

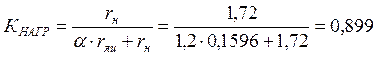2.3 Расчет передаточной функции тахогенератора

Передаточная функция тахогенератора имеет вид:

 

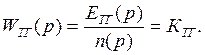
Для расчета воспользуемся данными, приведенными в таблице 3 и получим:

.

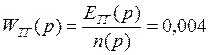2.4 Расчет передаточной функции системы

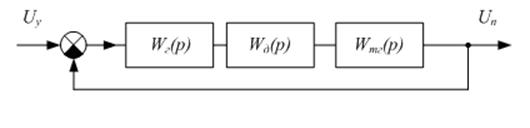
Рисунок 3− Структурная схема заданной системы

Согласно структурной схеме системы генератор, двигатель и тахогенератор соединены последовательно, значит передаточная функция системы примет вид:

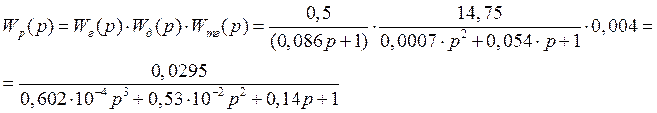
Передаточная функция замкнутой системы будет иметь вид:

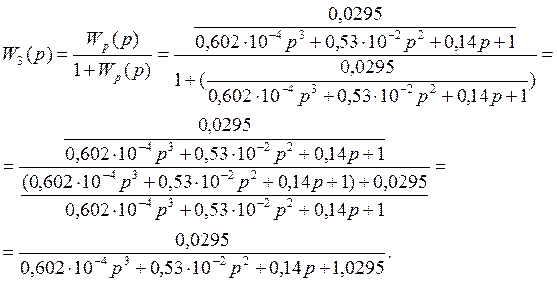
3 Анализ устойчивости АСР

3.1 Определение устойчивости системы

Выпишем характеристическое уравнение системы:

.

Для определения устойчивости АСР воспользуемся частным случае критерия Гурвица для систем третьего порядка, т.е. произведение внутренних коэффициентов  характеристического уравнения должно быть больше произведения крайних:

Вывод: Система в замкнутом состояние является устойчивой, т.к. произведение внутренних коэффициентов характеристического уравнения больше произведения крайних.

3.2 Определение критического коэффициента усиления системы

Для определения критического коэффициента усиления необходимо в главный определитель Гурвица вместо коэффициента  подставить К_кр+1, если система статическая, или К_кр, если система астатическая.

Так как данная система статическая, то выражение будет иметь вид:

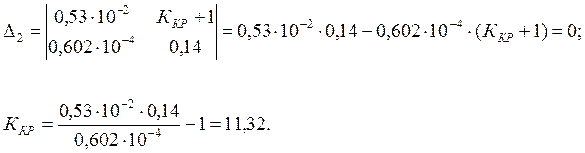
По заданной статической точности рассчитаем коэффициент усиления:

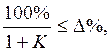
где ∆% - заданная статическая точность системы в процентах.

.

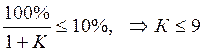Так как найденный по данной формуле К меньше К_кр , то необходимо произвести предварительную коррекцию АСР с целью дальнейшего облегчения синтеза корректирующего устройства, путем последовательного включения в систему пропорционального звена с коэффициентом:

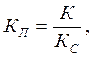
где К_с− расчетный коэффициент усиления АСР, равный произведению, , .

4 Построение переходного процесса по вещественной частотной характеристике замкнутой системы

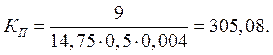
4.1 Построение ВЧХ

Для построения ВЧХ в передаточной функции замкнутой системы произведем замену p = jw:

.

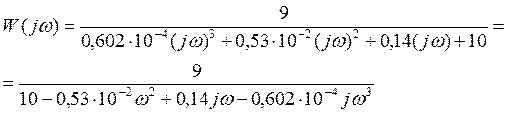Преобразуем полученное выражение:

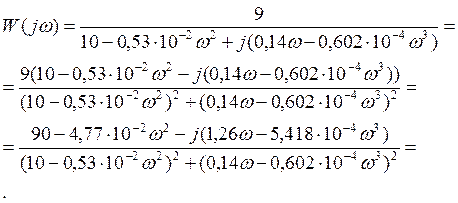
Из полученного выражения выделим вещественную часть:

.

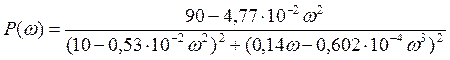Подставляя в полученное уравнение ВЧХ значение  от 0 до  найдем . Данные сводим в таблицу 4.

Таблица 4 − Данные ВЧХ заданной системы

w	0	12	23	32	37	40	42,7	43	43,8	44,2	44,6	45,4	46,9	48	50	55	63	72	82	112	120
P(w)	0,9	0,95	1,14	1,63	2,39	3,45	4,77	4,57	3,60	2,42	0,98	-1,55	-2,89	-2,65	-2,01	-1,08	-0,54	-0,31	-0,19	-0,06	-0,05