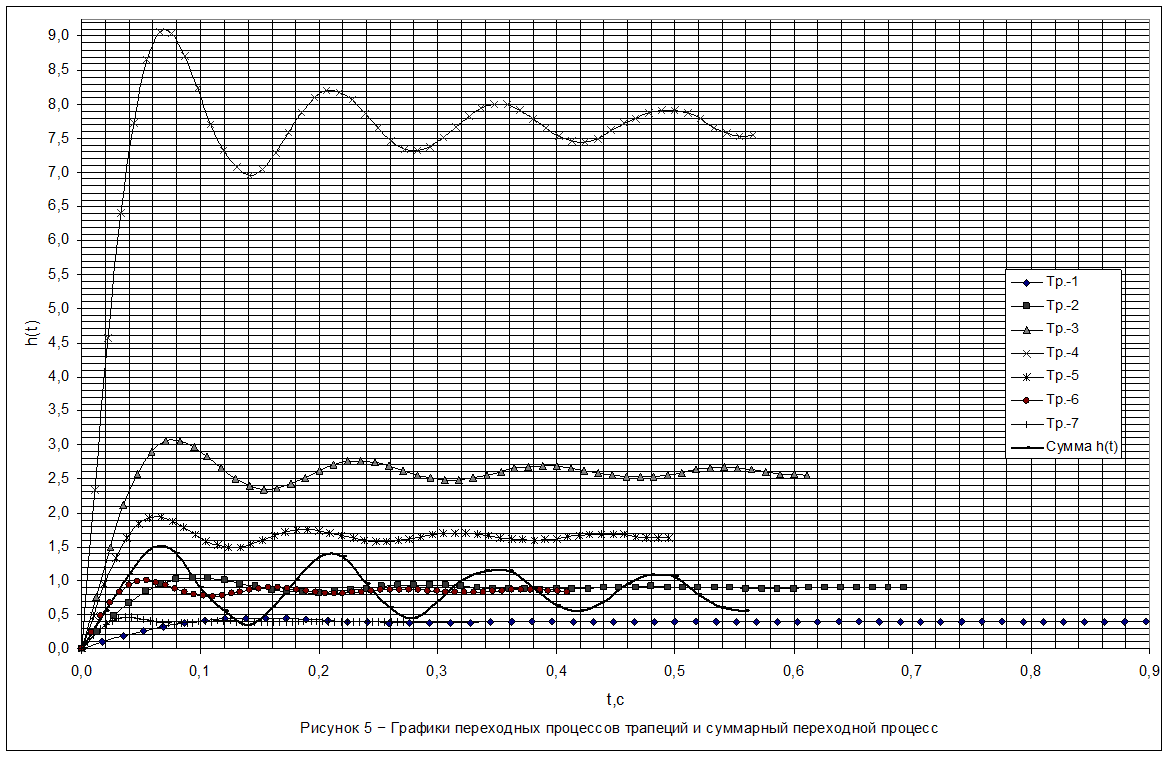
Построим графики переходных процессов с помощь ПП VisSim.
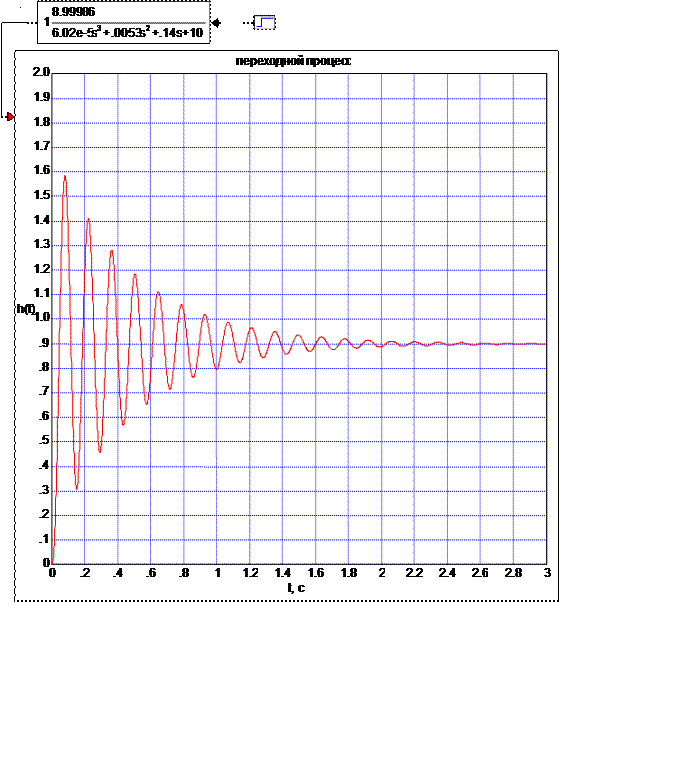
Рисунок 6 − Переходной процесс, построенный с помощью ПП VisSim
Анализ
полученных результатов: График суммарного переходного процесса, полученный в
результате разбиения ВЧХ замкнутой системы на трапеции, аналогичен графикам
построенным с помощью ПП VisSim. Небольшие расхождения в полученных результатах
объясняются, из-за несовершенства разбивки ВЧХ на трапеции и погрешностью
графического построения, суммарной переходной характеристики ![]() .
.
4.4 Анализ качества процесса регулирования
Анализ качества процесса регулирования проведем на основание прямых показателей качества для более точных результатов воспользуемся графиком на рисунке 6.
1) Вид переходного процесса:
Колебательный, затухающий.
2) Установившееся значение регулируемой величины:
![]() .
.
3) Максимальное отклонение регулируемой величины:
![]() .
.
4) Время регулирования:
![]() с.
с.
5) Перерегулирование:
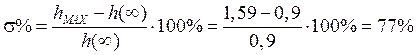 .
.
6) Степень затухания:
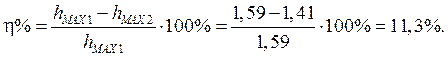
7) Логарифмический декремент затухания:
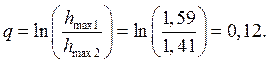
Анализ полученных результатов: Полученные показатели качества не соответствуют заданным, т.к. время регулирования превышает заданное, перерегулирование и степень затухания не соответствуют удовлетворительному качеству процесса регулирования.
5 Синтез АСР методом логарифмических частотных характеристик
5.1 Построение логарифмической амплитудной частотной характеристики (ЛАЧХ) исходной некорректированной системы
Разомкнутая система представляет собой последовательное соединение типовых звеньев генератора, двигателя, тахогенератора и звена предварительной коррекции:
![]() .
.
ЛАЧХ системы будет представлять собой сумму ЛАЧХ этих звеньев:
![]() .
.
5.1.1 ЛАЧХ двигателя
Для построения логарифмической амплитудно-частотной характеристики двигателя необходимо проверить выполнение условия:
![]() >
>![]()
Передаточная функция двигателя:
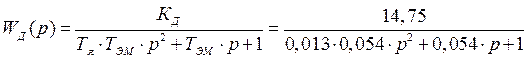 .
.
![]() <
<![]()
Условие не выполняется, следовательно двигатель является инерционным звеном второго порядка.
Из передаточной функции определим параметры логарифмической амплитудно-частотной характеристики
Определим амплитуду:
![]() .
.
Определим частоты сопряжения:
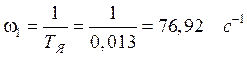 .
.
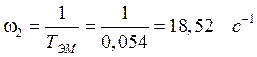
5.1.2 Определим ЛАЧХ генератора
Передаточная функция генератора имеет вид:
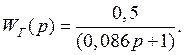
Генератор представляет собой инерционное звено первого порядка.
Определим амплитуду:
![]() .
.
Определим частоту сопряжения:
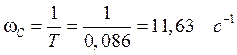 .
.
5.1.3 ЛАЧХ тахогенератора
Передаточная функция тахогенератора:
![]() .
.
Тахогенератор представляет собой пропорциональное звено, ЛАЧХ данного звена это прямая параллельная оси частот:
![]() .
.
5.1.4 ЛАЧХ звена предварительной коррекции
Передаточная функция:
![]() .
.
Звено предварительной коррекции, также как тахогенератор представляет собой пропорциональное звено, ЛАЧХ данного звена это прямая параллельная оси частот:
Определим амплитуду:
![]() .
.
5.2 Графическое построение ЛАЧХ каждого звена системы и ЛАЧХ некорректированной системы
По полученным данным выполним графическое построение ЛАЧХ каждого звена системы на одной плоскости.
Для построения ЛАЧХ некорректированной системы, произведем графическое суммирование ЛАЧХ всех звеньев системы:
![]() .
.
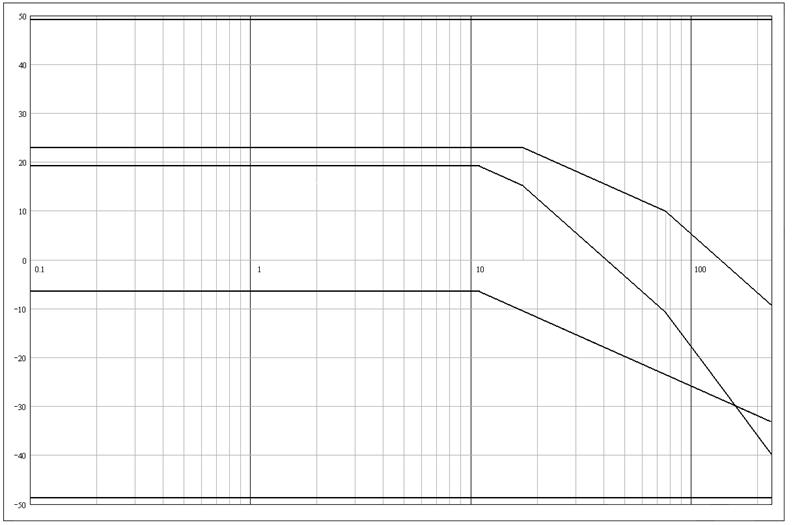
Рисунок 7 − ЛАЧХ звеньев системы и ЛАЧХ некорректированной системы
5.2 Построение желаемой ЛАЧХ ![]()
Желаемую ЛАЧХ строим на трех участках.
5.2.1 Построение участка низких частот
Данный участок характеризует статические свойства системы и ее точность в установившемся режиме. Так как данная система является статической ЛАЧХ будет представляет собой прямую параллельную оси частот.

Рисунок 8 − Желаемая ЛАЧХ на низких частотах
![]() ,
,
где К − коэффициент усиления, найденный из выражения:
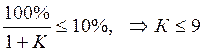 ,
,
![]()
5.2.2 Построение участка средних частот
Данный участок характеризует динамические свойства
системы, ее устойчивость и качество процесса регулирования. На участке средних
частот ЛАЧХ имеет наклон −20 дб/дек. и проходит через частоту среза ![]() и ограничен
запасом устойчивости по амплитуде
и ограничен
запасом устойчивости по амплитуде ![]() .
.
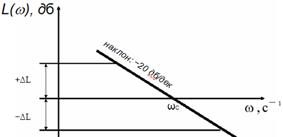
Рисунок 9 − Желаемая ЛАЧХ на средних частотах
Для нахождения частоты среза воспользуемся номограммой
приведенной в учебнике [6, страница 187]. Для заданного перерегулирования s%![]() 25% по номограмме определяем время
регулирования
25% по номограмме определяем время
регулирования 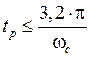 . По заданному времени
регулирования
. По заданному времени
регулирования ![]() с. находим частоту среза:
с. находим частоту среза:
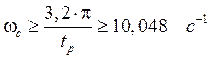 .
.
По той же номограмме определяем: Рmax=1,2 и Рmin=1− Рmax= −0,2.
По круговой диаграмме, построенной в логарифмическом
масштабе приведенной в учебнике [6, страница 188], определяем запас
устойчивости по амплитуде: ![]() дб, который ограничивает участок средних частот.
дб, который ограничивает участок средних частот.
Для определения точного значения частоты
в точках ![]() и
и ![]() составим
и решим логарифмическое уравнение:
составим
и решим логарифмическое уравнение:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.