Задаваясь значениями частоты от нуля до бесконечности находим значения Р(ω), данные заносим в таблицу 4.
Таблица 4 – Данные для построения ВЧХ замкнутой системы
|
ω |
0 |
2 |
4 |
5 |
6,2 |
8 |
10 |
12 |
15 |
20 |
23 |
+∞ |
|
Р(ω) |
0,32 |
0,317 |
0,187 |
-0,07 |
-0,26 |
-0,18 |
-0,01 |
-0,06 |
-0,03 |
-0,008 |
-0,004 |
0 |
По данным таблицы 4 строим ВЧХ замкнутой системы (рисунок 3).
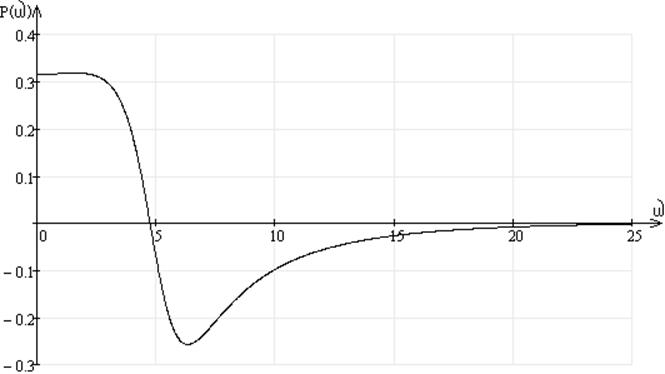
Рисунок 3 – ВЧХ замкнутой системы
1.5.1 Разбивка ВЧХ на трапеции
К полученной ВЧХ замкнутой системы применим правила разбивки на трапеции, определим параметры трапеций и представим их в виде таблицы. При разбивки на трапеции следует помнить, что все трапеции должны одной стороной прилегать к оси ординат, а также что должно выполняться равенство

где ri – высота i-й трапеции; P(0) – значение P(ω) при ω=0.
Коэффициент наклона рассчитываем по формуле

где ωс – частота среза, ωd – динамическая частота.
Переход от табличной величины функции h(τ) к реальному ее значению h(t) производится по формуле

где r – высота
трапеции; t – реальное
время, с,
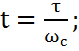 τ – табличное значение времени, с; ωс –
частота среза реальной трапеции.
τ – табличное значение времени, с; ωс –
частота среза реальной трапеции.
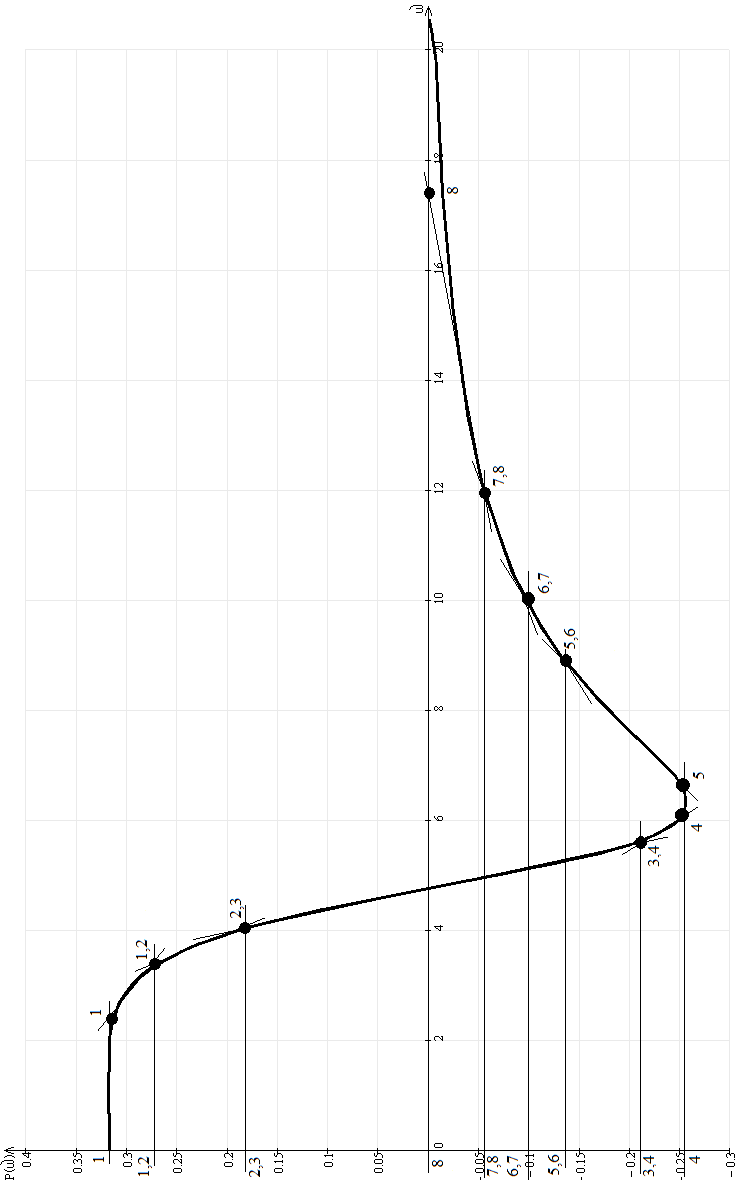
Разбиваем вещественную частотную характеристику системы на трапеции (рисунок 4).
Составим уравнение трапеций
![]()
Рассчитаем параметры трапеций и занесем их в таблицу 5.
Таблица 5 – Параметры трапеций
|
Тр1 |
Тр2 |
Тр3 |
Тр4 |
Тр5 |
Тр6 |
Тр7 |
Тр8 |
|
|
ωd |
2.61 |
3.43 |
4.09 |
5.61 |
6.69 |
8.78 |
10 |
11.87 |
|
ωc |
3.43 |
4.09 |
5.61 |
6.17 |
8.78 |
10 |
11.87 |
17.57 |
|
χ |
0.76 |
0.84 |
0.73 |
0.91 |
0.76 |
0.88 |
0.84 |
0.68 |
|
r |
0.05 |
0.09 |
0.39 |
0.05 |
-0.12 |
-0.04 |
-0.04 |
-0.06 |
![]()

1.6 Построение переходного процесса системы
1.6.1 Построение переходного процесса методом трапеций
Для каждой трапеции, используя таблицу h-функций, рассчитываем значения h(t)-функций используя выражение (5) и формулу

Результаты вычислений заносим в таблицу 6 для 1, 2, 3 и 4 трапеций, и в таблицу 7 для 5, 6, 7 и 8 трапеций.
По данным таблиц 6 и 7 на одной плоскости строим переходные процессы для каждой из трапеций (для каждой части ВЧХ) и графически, путем суммирования ординат на основании уравнения ВЧХ, находим переходную характеристику системы (рисунок 5).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
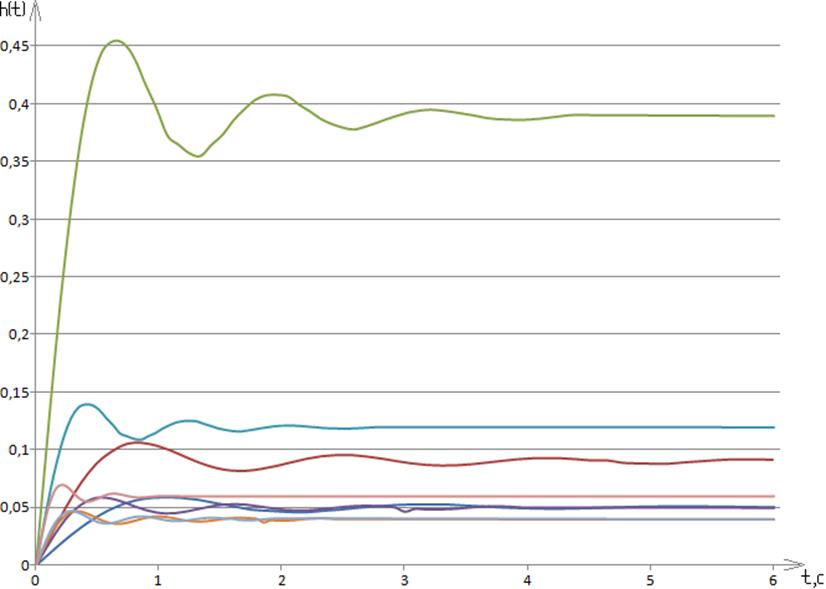
Рисунок 5 – Переходные процессы трапеций и всей системы
Таблица 6 – Значения h(t)-функции для 1, 2, 3 и 4 трапеций
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.