Тэм – электромеханическая постоянная времени;
Кд – коэффициент передачи двигателя по управляющему воздействию.
Определим для двигателя П-11 параметры передаточной функции при номинальном потоке возбуждения. Принимаем приведенный момент инерции нагрузки Iп равным моменту инерции якоря двигателя Iд.
Для численного выражения момента инерции I в единицах СИ через маховый момент GD2, кГ×м2 , воспользуемся соотношением (2)

Найдем значения Iя. ном, rя.ц и Iд
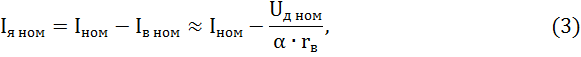
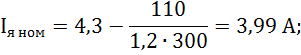
![]()
![]()

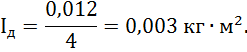
Далее определяем постоянные для двигателя
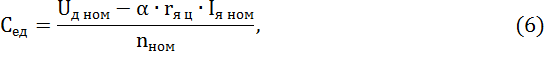
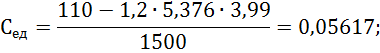

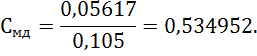
Последнее равенство справедливо для случая, когда момент сопротивления на валу двигателя не зависит от скорости вращения. Оно получено в результате преобразования следующих соотношений:

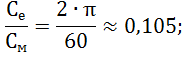
![]()
Вычислить индуктивность якоря Lя сложно, поэтому на практике ее определяют экспериментально. Находим величину Lя приближенно

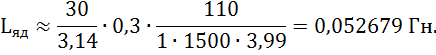
Момент инерции на валу двигателя
![]()
![]()
Подставив численные значения найденных параметров в коэффициенты передаточной функции двигателя, получим коэффициент по управляющему воздействию

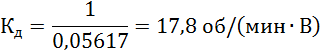
и постоянные времени

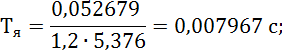

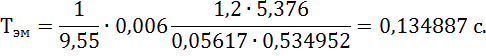
Передаточная функция двигателя имеет вид
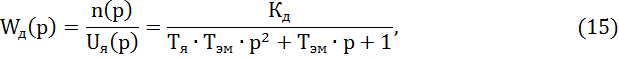
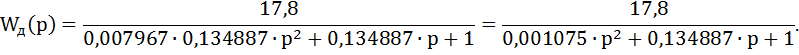
1.2.2 Определение передаточной функции ЭМУ
Передаточная функция ЭМУ в общем виде
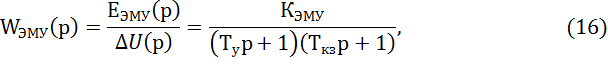
где ЕЭМУ – ЭДС электромашинного усилителя;
КЭМУ – коэффициент передачи ЭМУ по напряжению;
Ту – постоянная времени цепи управления;
Ткз - постоянная времени короткозамкнутой (к.з.) цепи.
Определяем индуктивность обмотки управления
![]()
Находим постоянную времени ЭМУ

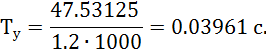
Коэффициент передачи ЭМУ в режиме холостого хода приближенно можно найти по номинальным данным
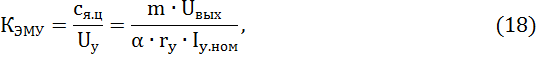
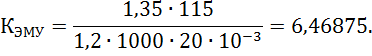
Передаточная функция ЭМУ
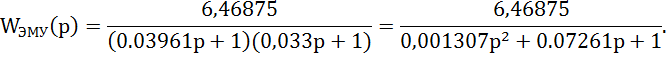
1.2.3 Определение передаточной функции тахогенератора
Передаточная функция тахогенератора в общем виде

где ![]()
![]()
1.3 Определение передаточной функции АСР
Структурная схема системы представленная на рисунке 2.

Рисунок 2 – Структурная схема АСР
ЭМУ включен с двигателем последовательно. Передаточная функция ЭМУ с двигателем имеет вид
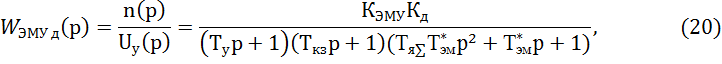
где Тя∑ - суммарная постоянна времени цепи якоря ЭМУ и двигателя, с;

![]() ̶ электромеханическая постоянная времени двигателя
при работе от ЭМУ, с;
̶ электромеханическая постоянная времени двигателя
при работе от ЭМУ, с;
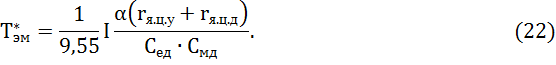
Величину индуктивности цепи якоря ЭМУ Lяу находим приближенно по формуле (10), принимая β=0,25
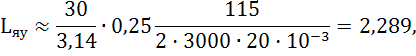
![]()
![]()
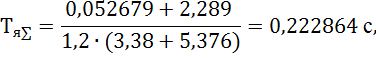
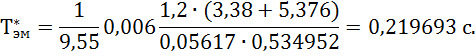
Передаточная функция ЭМУ с двигателем
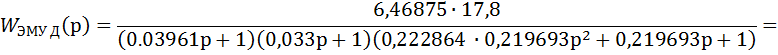
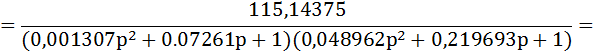
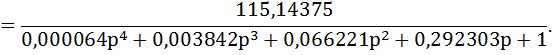
Тахогенератор соединен с двигателем и ЭМУ последовательно, и передаточная функция разомкнутой системы примет вид
![]()
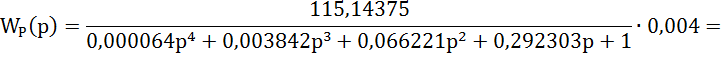
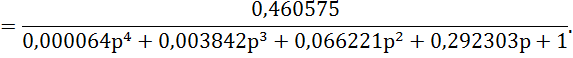
Передаточная функция замкнутой системы

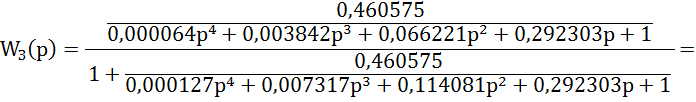
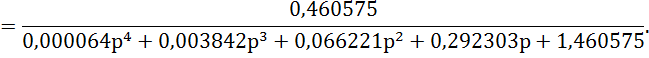
1.4 Исследование устойчивости АСР
Устойчивость системы будем определять по алгебраическому критерию Гурвица: для того чтобы система была устойчивой, необходимо и достаточно, чтобы главный определитель Гурвица и все диагональные миноры были положительны.
Характеристическое уравнение системы имеет вид
![]() .
.
Правило Стодолы выполняется: все коэффициенты характеристического уравнения положительные, то есть одного знака.
Найдем главный определитель Гурвица и диагональные миноры
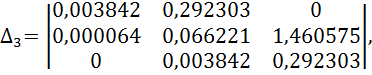
![]()
![]() ;
;
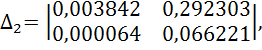
![]()
![]()
![]()
Исследуемая система устойчива, так как главный определитель Гурвица и все диагональные миноры положительны.
1.4.1 Расчет критического коэффициента усиления
Для расчета критического коэффициента усиления в определителе Гурвица вместо a4 поставим Ккр+1 (так как система статическая) и приравняв определитель к нулю найдем Ккр
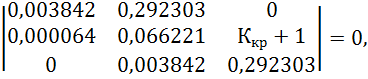
![]()
![]()
![]()
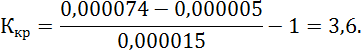
1.4.2 Расчет необходимого коэффициента усиления
По заданной статической точности найдем необходимый коэффициент усиления из выражения

где ![]() - заданная статическая точность системы, %.
- заданная статическая точность системы, %.
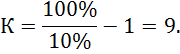
В предварительной коррекции АСР нет необходимости, так как найденный коэффициент К больше критического коэффициента Ккр.
1.5 Построение ВЧХ замкнутой системы
Известно, что между h(t) и ВЧХ замкнутой системы существует связь,
которая определяется интегралом
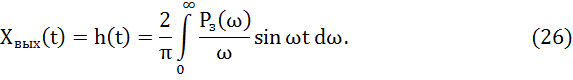
Для построения ВЧХ замкнутой системы в передаточной функции сделаем
подстановку р=jω и домножив на сопряженное выделим вещественную часть
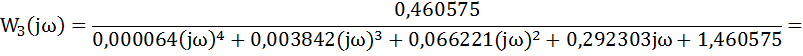
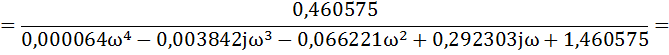
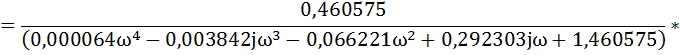
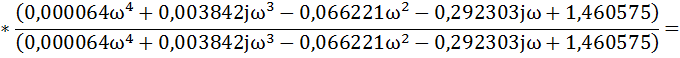
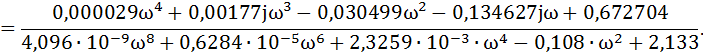
Выделим вещественную часть
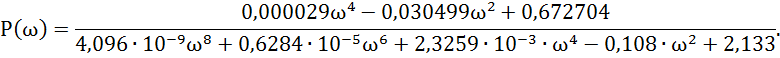
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.