Цель работы: Исследование автоколебательных процессов в нелинейной системе, влияние вида нелинейности на качество нелинейной системы.
Гармоническая линеаризации основана на том, что в рассматриваемой нелинейной системе устанавливается режим некоторого периодического движения с заранее неизвестными амплитудой A и частотой w.
Периодический выходной сигнал нелинейного звена можно разложить в ряд Фурье:
|
|
(16) |
где
|
|
(17) |
|
|
|
(18) |
|
|
|
(19) |
При наличии свойства фильтра линейная часть системы будет хорошо пропускать первую гармонику нелинейных колебаний и ослаблять все высшие гармоники. Поэтому переменная на входе нелинейного звена окажется близкой к синусоиде:
|
|
(20) |
Таким образом, в нелинейной системе могут существовать автоколебания, и задача исследования сводится к определению двух неизвестных: частоты w и амплитуды A первой гармоники в случае симметричных колебаний.
Для решения данной задачи можно использовать метод гармонической линеаризации, заключающийся в представлении передаточной функции нелинейного звена в гармонически линеаризованном виде:
|
|
(21) |
При этом коэффициенты гармонической линеаризации определяются по следующим выражениям:
|
|
(22) |
|
|
|
(23) |
Определение частоты и амплитуды симметричных автоколебаний в нелинейной АСР (рис. 20) можно провести частотным способом.
|
|
|
Рис. 20. Структурная схема АСР |
Рассчитываются и строятся на комплексной плоскости годографы Михайлова и нелинейной части.
Годограф линейной части находится обычным методом, путем замены s = jw в передаточной функции Wл. Годограф нелинейного звена рассчитывается по гармонически линеаризованной передаточной функции:
|
|
(24) |
Точка пересечения годографов определяет величины A и w,
причем значение амплитуды определяется по обратной амплитудной характеристике
нелинейного звена 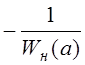 , а значение частоты – по
, а значение частоты – по ![]() .
.
Проверку на устойчивость полученного решения можно осуществлять с помощью алгебраического критерия устойчивости:
|
|
(25) |
В случае выполнения неравенства в системе существуют устойчивые симметричные автоколебания, в противном случае будут неустойчивые расходящиеся колебания, что свидетельствует о неустойчивости всей системы.
Практическое задание:
1. Найти АФЧХ линейной части.
2. Найти обратную амплитудную характеристику нелинейного элемента.
3. Построить эти две характеристики на одном графике в Mathcad.
4. Сделать вывод об устойчивости автоколебаний в системе в случае их наличия.
Методика выполнения работы:
1. Согласно варианту задания (табл.6, прил.1) определите передаточную функцию линейной части нелинейной системы Wл(s).
2. Сделав замену s = jw выделите вещественную (P(w)) и мнимую (Q(jw)) часть. Постройте график АФЧХ в Mathcad.
3. Согласно варианту задания (табл.6, рис.21) по статической характеристике нелинейного элемента рассчитайте коэффициенты гармонической линеаризации q(a) и q’(a).
4. Определите передаточную функцию нелинейного элемента Wн(a).
5. Найдите и
постройте в Mathcad обратную амплитудную характеристику
нелинейного элемента 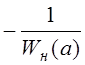 .
.
6. Постройте обе характеристики на одном графике и сделайте выводы о наличии автоколебательного режима в системе. В случае наличия автоколебаний сделайте вывод об их устойчивости.
Таблица 6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.