КАЧЕСТВО ПРОЦЕССОВ В ЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМАХ
Основные показатели качества процессов в импульсных системах такие же, как и в непрерывных автоматических системах: время регулирования tp,, величина перерегулирования σ и число перерегулирований (показатели качества переходного процесса); точность работы систем в установившихся режимах.
Но имеются особенности исследования качества ИС.
Аналог интегральных оценок
Интегральные оценки исследования качества ИС, по аналогии с линейными системами, позволяют оценить длительность переходного процесса, а также суммарные отклонения регулируемой величины от установившегося значения.
Динамические свойства переходного процесса в системе с АИМ можно охарактеризовать интегральными оценками вида:
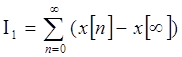 - аналог первой интегральной
оценки;
- аналог первой интегральной
оценки;
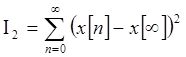 - аналог квадратичной интегральной
оценки,
- аналог квадратичной интегральной
оценки,
здесь
![]() - установившееся значение
регулируемой величины (либо сигнал ошибки, либо
статическое отклонение):
- установившееся значение
регулируемой величины (либо сигнал ошибки, либо
статическое отклонение):
![]() .
.
В
ИС часто ![]()
![]() .
.
Поэтому
используют: 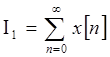
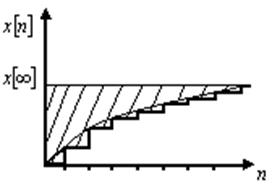
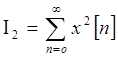
Оценка ![]() определяет
площадь, заключенную между графиком ступенчатой функции, образующейся из
решетчатой функции
определяет
площадь, заключенную между графиком ступенчатой функции, образующейся из
решетчатой функции ![]() , и графиком ее
установившегося значения (т. е. площадь отклонения ступенчатой функции от ее
предельного значения).
, и графиком ее
установившегося значения (т. е. площадь отклонения ступенчатой функции от ее
предельного значения).
Оценка
![]() применяется только для
неколебательных процессов.
применяется только для
неколебательных процессов.
Используя
теорему о площади при ![]()
![]() выражение
выражение
![]() :
:
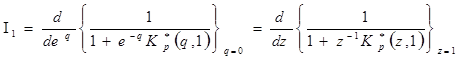 ,
,
где
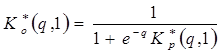 .
.
Оценку ![]() можно
использовать для любых процессов. Оценку
можно
использовать для любых процессов. Оценку ![]() вычисляют
непосредственно по коэффициентам передаточной функции замкнутой ИС.
вычисляют
непосредственно по коэффициентам передаточной функции замкнутой ИС.
Например:
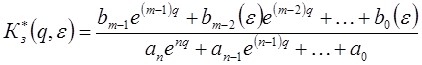
при
![]()
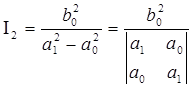 ,
,
формулы
при ![]() и т. д. см. литературу.
и т. д. см. литературу.
Оценку
![]() также можно определить по
частотной характеристике замкнутой ИС:
также можно определить по
частотной характеристике замкнутой ИС:
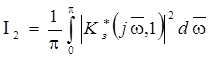 .
.
Корневые показатели
1)
степень
устойчивости α – это минимальная вещественная часть корня
характеристического уравнения ![]() .
.
Т.
к. исследуемые процессы выражаем через относительное время, то величина ![]() является относительной величиной.
является относительной величиной.
Абсолютная
степень устойчивости: ![]() .
.
Как
известно степень устойчивости связана с длительностью переходного процесса: чем
ниже α, тем меньше затухание и тем больше ![]() –
длительность переходного процесса.
–
длительность переходного процесса.
Время
регулирования можно оценить по приближенной формуле ![]() ;
;
![]() – это относительное время
устойчивости.
– это относительное время
устойчивости.
Для
нахождения ![]() поступают следующим
образом:
поступают следующим
образом:
в
характеристическое уравнение ![]()
делают
замену ![]() и получают уравнение
и получают уравнение
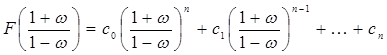
и после преобразований получают характеристическое уравнение относительно параметра ω:
![]() .
.
Далее
делают замену: ![]() . В результате получают
характеристическое уравнение некоторой фиктивной системы, у которой граница
устойчивости смещена влево на величину
. В результате получают
характеристическое уравнение некоторой фиктивной системы, у которой граница
устойчивости смещена влево на величину ![]() .
.
Задача заключается в нахождении параметров, при которых фиктивная система находится на границе устойчивости. Исследование устойчивости этой системы может быть проведено по любому из критериев, например критерий Гурвица.
Приравнивания
главный определитель Гурвица к нулю, находят ![]() ,
наименьшая из которых будет являться искомой степенью устойчивости.
,
наименьшая из которых будет являться искомой степенью устойчивости.
2)
колебательность ![]() – это абсолютное
значение отношения мнимой части к действительной части корня
характеристического уравнения, ближайшего к мнимой оси:
– это абсолютное
значение отношения мнимой части к действительной части корня
характеристического уравнения, ближайшего к мнимой оси: ![]() , где
, где ![]() .
.
Колебательность
позволяет оценить качество переходного процесса: чем больше ![]() , тем дольше происходит затухание
переходного процесса.
, тем дольше происходит затухание
переходного процесса.
![]() можно определить путем замены в
характеристическом уравнении ω на выражение:
можно определить путем замены в
характеристическом уравнении ω на выражение: 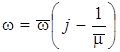 .
.
После
проведения этой замены находят по критерию Гурвица границу устойчивости,
приравняв определители к нулю. Из этих условий находят ![]() .
.
Точность ИС в установившемся режиме
Точность ИС оценивают по установившемуся значению сигнала ошибки.
По теореме о конечном значении оригинала дискретного преобразования Лапласа (из МОА) можно найти:
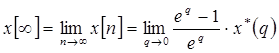 .
(1)
.
(1)
Необходимо найти предел ошибки, поэтому воспользуемся передаточной функцией ИС относительно ошибки:
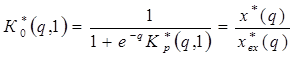
Из
нее выразим 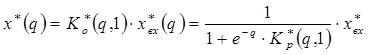 и подставим в
уравнение (1):
и подставим в
уравнение (1):
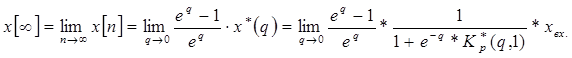 (2)
(2)
Это выражение справедливо для любого входного воздействия.
Если
на вход ИС подается единичное ступенчатое воздействие, т.е. 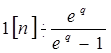 , то уравнение (2) будет:
, то уравнение (2) будет:
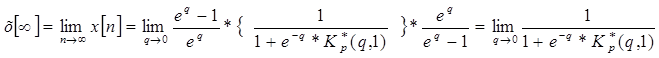 . (3)
. (3)
Для многих ИС ![]() (см. практику).
(см. практику).
Таким образом, по уравнениям (2) и (3) оценивают точность ИС в установившемся режиме.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.