График возмущающего воздействия DXвх (t), % ХРО представлен на рисунке 4.1.

Рисунок 4.1 – График возмущающего воздействия Xвх (t), % ХРО
График кривой разгона объекта – температура раствора NaOH в колонне десорбции ∆T(t), ºC представлен на рисунке 4.2.
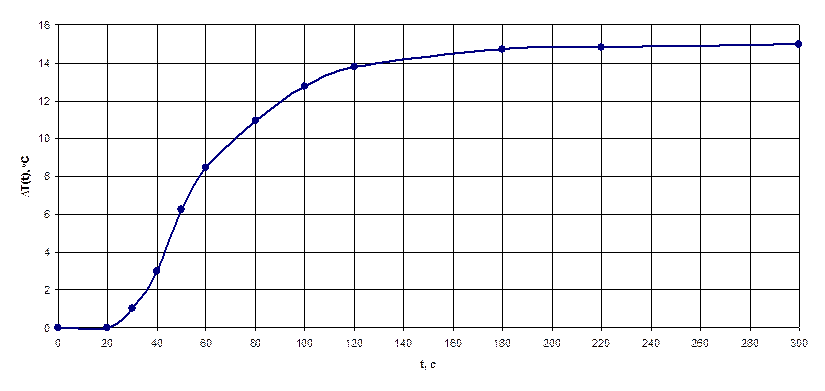
Рисунок 4.2 – График кривой разгона объекта ∆T(t), ºC
Единичная DT0(t) и нормированная DTН(t) переходные функции определяются по следующим формулам:
DT0(t) = DT(t) / A, (1)
DTН(t) = DT0(t) / DT0(Tу), (2)
где A – скачкообразное возмущающее воздействие, при котором снята переходная характеристика (А = 4 % ХРО);
Tу – время переходного процесса;
DTН(Tу) – установившееся значение переходной характеристики DT0(Tу) = 3,7375 ºC).
Результаты расчётов единичной и нормированной переходных функций сведены в таблицу 4.
Таблица 4 - Результаты расчётов единичной и нормированной переходных функций
|
t, c |
∆Т(t), ºC |
∆Т0(t), (ºC)/%ХРО |
∆Тн(t) |
|
0 |
0 |
0 |
0 |
|
20 |
0 |
0 |
0 |
|
30 |
1,05 |
0,2625 |
0,0702 |
|
40 |
3 |
0,75 |
0,2007 |
|
50 |
6,24 |
1,56 |
0,4174 |
|
60 |
8,45 |
2,1125 |
0,5652 |
|
80 |
10,92 |
2,73 |
0,7304 |
|
100 |
12,74 |
3,185 |
0,8522 |
|
120 |
13,78 |
3,445 |
0,9217 |
|
180 |
14,69 |
3,6725 |
0,9826 |
|
220 |
14,82 |
3,705 |
0,9913 |
|
300 |
14,95 |
3,7375 |
1 |
По результатам таблицы 10 строим на одном графике единичную, нормированную и экспериментальную переходные функции (рисунок 4.3).
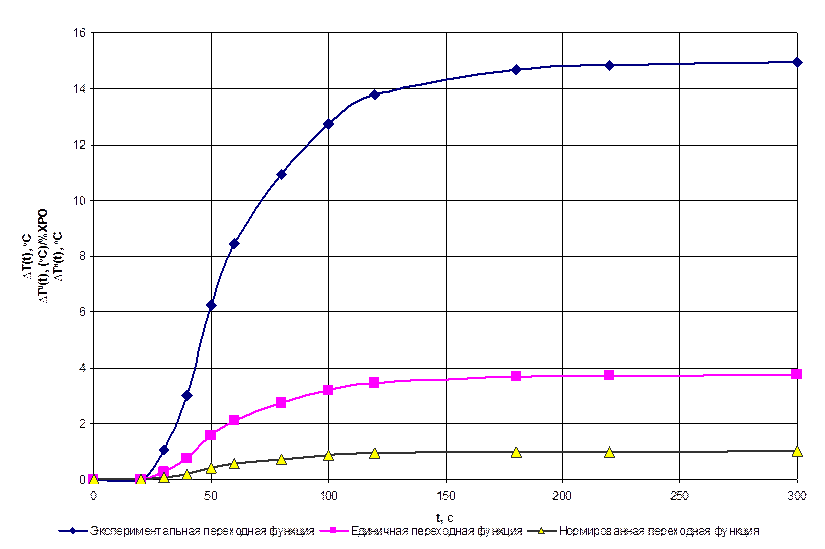
Рисунок 4.3 – Сравнительный анализ переходных процессов
Из зависимости ΔТ0(t) находим величину коэффициента усиления объекта Коб:
Kоб = DT0(Tу) = 3,7375 (3)
Динамические характеристики объекта при аппроксимации его последовательным соединением апериодического звена и звена запаздывания:
– транспортное запаздывание объекта определяется как отрезок времени (0; t), на котором выполняется неравенство 0 £ DTН(t) £ D,
где D = (0,01..0,02) DTН(tу); по графику на рисунке 3.2 определяем t = 20 с;
– дополнительное запаздывание tд находится по формуле:
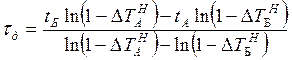 , (4)
, (4)
где
(tБ, ![]() ) и (tА,
) и (tА, ![]() ) – точки пересечения
аппроксимированной и экспериментальной кривыми разгона,
) – точки пересечения
аппроксимированной и экспериментальной кривыми разгона, ![]() =
(0,1÷0,15),
=
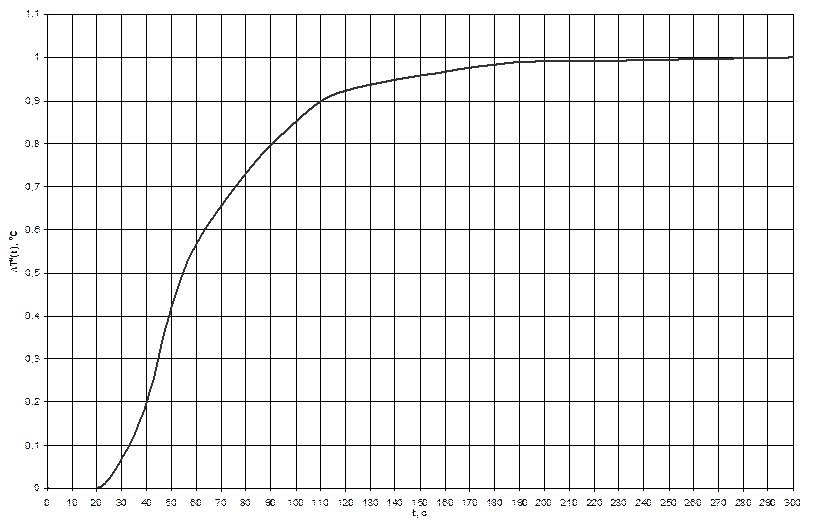
(0,1÷0,15), ![]() = (0,7÷0,85). Из tА и tБ исключено время
транспортного запаздывания. По графику на рисунке 4.4 определяем значения tА = 12,5 с., при
= (0,7÷0,85). Из tА и tБ исключено время
транспортного запаздывания. По графику на рисунке 4.4 определяем значения tА = 12,5 с., при ![]() = 0,1 и tБ = 56 с., при
= 0,1 и tБ = 56 с., при ![]() = 0,7.
= 0,7.
|
|
|
 |
Рисунок 4.4 – Анализ нормированного переходного процесса
Дополнительное запаздывание:
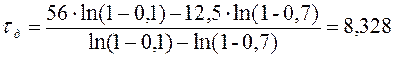 с;
с;
- общее запаздывание объекта:
tоб = t+ tд = 20 + 8,328= 28,328 с; (5)
- постоянная времени:
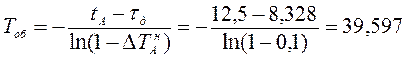 с. (6)
с. (6)
Таким образом, аппроксимирующая передаточная функция имеет вид:
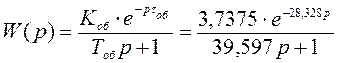 . (7)
. (7)
Для определения точности аппроксимации экспериментальной переходной функции решением дифференциального уравнения первого порядка с запаздывающим аргументом рассчитываются ординаты аппроксимирующей кривой:
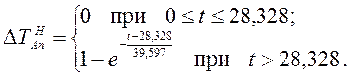 (8)
(8)
Для определения среднеквадратической ошибки аппроксимации вычисляется отношение dАп:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.