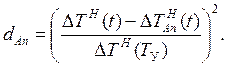Промышленность \ Автоматизация технологических процессов и производств

Автоматизация процесса осветления рабочей воды на ТЭЦ. Расчет линейной одноконтурной САР расхода промывочной воды при возмущении по нагрузке, страница 10

                                                                       (9)

Результаты расчетов приведены в таблице 5, а график аппроксимирующей кривой показан на рисунке 4.5.

Таблица 5 – Ординаты переходных функций

t, с

∆Тн(t)

∆Тна1(t)

0

0

0

0

20

0

0

0

30

0,0702

0,04135

0,00083

40

0,2007

0,25530

0,00298

50

0,4174

0,42150

0,00002

60

0,5652

0,55061

0,00021

80

0,7304

0,72881

0,00000

100

0,8522

0,83635

0,00025

120

0,9217

0,90125

0,00042

180

0,9826

0,97830

0,00472

220

0,9913

0,99210

0,00052

300

1

0,99895

0,02289

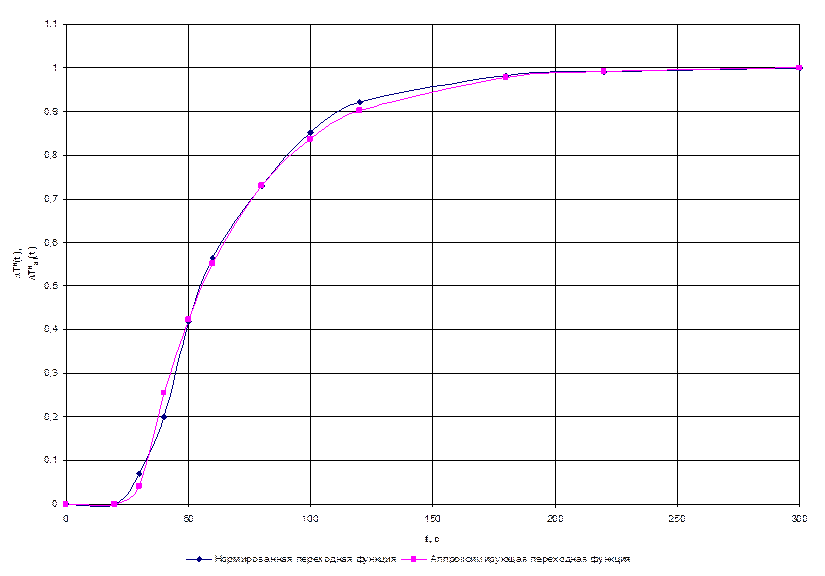
Рисунок 4.5 – Аппроксимация переходной функции решением дифференциального уравнения первого порядка

          По данным таблицы 11 рассчитываем среднеквадратичную ошибку аппроксимации δ:

%.

Погрешность аппроксимации удовлетворительная (δ ≤ 3 %). Поэтому окончательно принимаем аппроксимацию объекта дифференциальным уравнением первого порядка.

4.2 Выбор регулятора

Тип регулятора выбираем из таблицы 2.1 [1] по отношению:

.

Так как 0,2 <  < 1, выбираем непрерывный тип регулятора.

Для выбора закона регулирования рассчитываем динамический коэффициент регулирования:

.

По графику на рисунке 2.3в [1] определяем, что только ПИД-регулятор может обеспечить значение Rд=0,133 ниже расчётного для требуемого вида переходного процесса.

По графику на рисунке 2.4в [1] находим для ПИД-регулятора отношение , откуда время регулирования tр = 10∙τоб = 10∙28,328 = 283,28 с., что больше допустимого времени регулирования tр ≤ 250 с, и так как мы выбрали самый сложный закон регулирования (ПИД-закон), который обеспечивает наименьшее время регулирования из возможного, окончательно выбираем его.

4.3 Определение настроек регулятора

Расчет настроек выбранного регулятора выполняют следующим способом:

-  графо-аналитическим на основе амплитудно-фазовой характеристики;                    

-  объекта и М-критерия (показателя колебательности);

-  по расширенным амплитудно-фазовым характеристикам;

-  по приближенным формулам;

-  с помощью математического моделирования.

На практике настройки регуляторов определяют обычно по приближённым формулам (таблица 2.2 [1]), а затем производят их уточнение.

Настройки ПИД-регулятора по приближённым формулам имеют следующие значения:

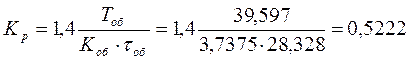 %ХРО/ºС,

 с,

 с.

Уточнение настроек регулятора произведём в среде MATLAB 6.5, с помощью встроенного пакета Simulink. Модель автоматической системы регулирования в Simulink представлена на рисунке 4.6.

Для задания настроек встроенного в Simulink ПИД-регулятора необходимо перевести значения времени интегрирования и времени предварения в значения коэффициентов интегральной и дифференциальной составляющих ПИД-закона регулирования:

-  коэффициент пропорциональной составляющей p = Kп = 0,5222;

-  коэффициент интегральной составляющей i = Kр/Tи = 0,014;

-  коэффициент дифференциальной составляющей d = Kр∙Tд = 7,396.

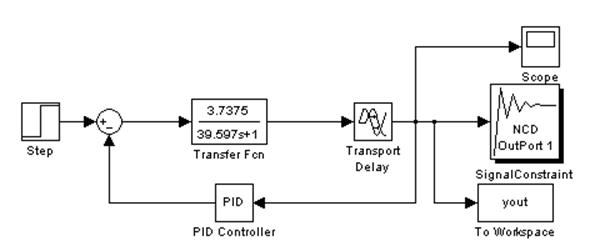
Рисунок 4.6 – Модель автоматической системы регулирования в Simulink

При задании в командной строке MATLAB 6.5 значений коэффициентов составляющих закона регулирования:

>> p=0,5222;

>> i=0,014;

>> d=7,396.

При моделировании в Simulink получается переходной процесс, изображённый на рисунке 4.7.

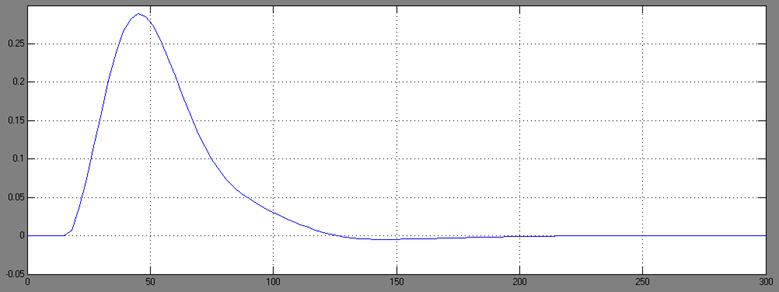
Рисунок 4.7 – Переходной процесс при исходных настройках регулятора

Для оптимизации настроек регулятора необходимо в блоке Signal Constraint задать ограничения на вид переходного процесса, указать параметры p, i и d в качестве настраиваемых. После этого можно запустить процесс оптимизации. В результате получается переходный процесс, изображённый на рисунке 4.8, по заданию процесс с .

Скачать файл