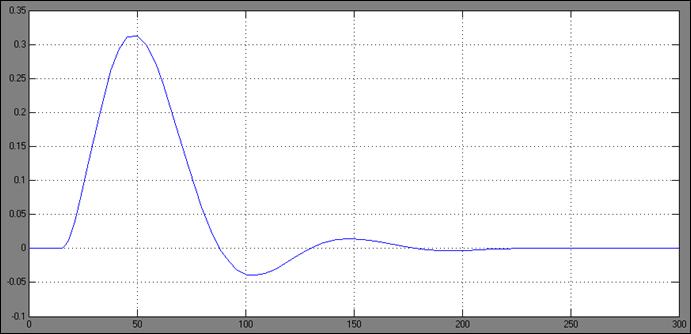
Промышленность \ Автоматизация технологических процессов и производств

Автоматизация процесса осветления рабочей воды на ТЭЦ. Расчет линейной одноконтурной САР расхода промывочной воды при возмущении по нагрузке, страница 11

Рисунок 4.8 – Переходной процесс при оптимальных настройках регулятора

Для получения значений настроек регулятора в командной строке MATLAB 6.5 вводится команда:

>> p, i, d.

В результате в рабочее окно будут выведены оптимизированные значения настроек регулятора:

p = 0,57;

i = 0,016;

d = 8,17;

В результате оптимизации были получены следующие настройки ПИД-регулятора:

-  коэффициент усиления регулятора Kр = p = 0,57 %ХРО/ ºС;

-  время изодрома Tи = p/i = 35,625 с;

-  время предварения Tд = d/p = 14,3 с.

Окончательно передаточная функция регулятора будет иметь вид:

.

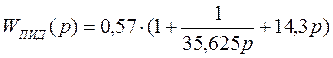4.4  Определение устойчивости АСР

Проверим рассчитанную АСР на устойчивость с помощью п/п MATLAB 6.5 и пакета Control System Toolbox, который является одним из основных инструментариев разработчика систем управления в среде MATLAB 6.5. Это сборник алгоритмов MATLAB для моделирования, анализа и проектирования СУ. В пакете используются как и традиционные методы ТАУ с использованием передаточных функций, так и современные методы с использованием пространства состояния.

Основные свойства пакета Control System:

формы представления

·  непрерывные и дискретные СУ.

·  форматы моделей: передаточные функции (ПФ), пространство состояний (ПС), нули-полюса (НП).

·  построение линейных моделей СУ.

·  преобразование моделей в различные форматы: ПФ, НП, ПС.

анализ

·  полный набор средств для анализа одно- (SISO) и многомерных (MIMO) систем.

·  временные характеристики: переходная и импульсная переходная характеристики, реакция системы на произвольное воздействие.

·  частотные характеристики: диаграммы Боде (АЧХ, ФЧХ), Найквиста и Никольса (АФХ) и др..

проектирование

·  расчет параметров обратной связи.

·  проектирование линейно-квадратичных регуляторов (LQR).

·  характеристики моделей: управляемость, наблюдаемость, понижение порядка модели.

·  поддержка систем с запаздыванием.

Пакет часто используется совместно с другими пакетами MATLAB для проектирования более сложных СУ.

Итак, в рабочем окне программы вводим специальные команды, задаем передаточную функцию объекта управления, ПИД-регулятора и охватываем объект обратной связью по аналогии с рисунком 4.6. С помощью встроенных средств строим годограф Найквиста (рисунок 4.9). Листинг команд, использованных при работе с MATLAB, представлен ниже:

>> w1=tf(3.7375,[39.597 1],'inputdelay',28.328)

Transfer function:

                          3.737

exp(-28.3*s) * ----------

                       39.6 s + 1

>> w2=pade(w1,1)

Transfer function:

     -3.737 s + 0.2639

---------------------------

39.6 s^2 + 3.796 s + 0.0706

>> pid=tf([290.38 20.3 0.57],[35.625 0])

Transfer function:

290.4 s^2 + 20.3 s + 0.57

-------------------------

         35.63 s

>> s=feedback(w2,pid)

Transfer function:

          -133.1 s^2 + 9.4 s

--------------------------------------

325.3 s^3 + 136 s^2 + 5.741 s + 0.1504

>> nyquist(s)

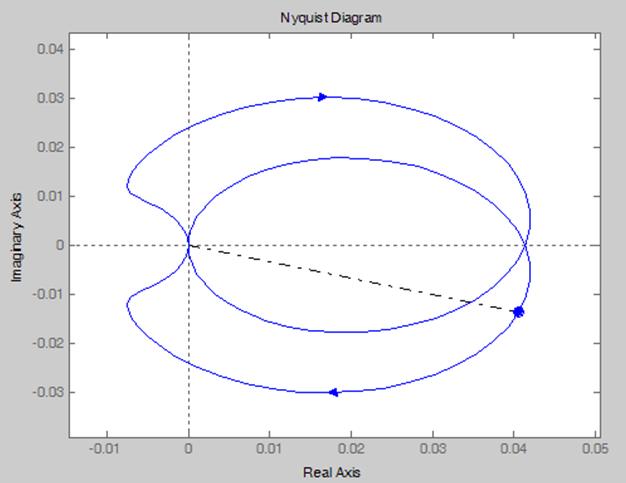
Рисунок 4.9 – Годограф Найквиста

Как видно из рисунка, годограф не охватывает точку с координатой (-1; j0), значит система устойчива. АСР также обладает достаточным запасом устойчивости по амплитуде и по фазе.

4.5  Проверка системы на оптимальность

Для того, чтобы убедиться в правильности нахождения настроек регулятора, изменим настройки ПИД – регулятора на 20 % в большую сторону (КП = 0,684 ХРО/ºC; ТИ =42,75 с; ТД = 17,16 с), и в меньшую сторону (КП = 0,456 %ХРО/ ºC; ТИ= 28,5 с; ТД = 11,44 с).

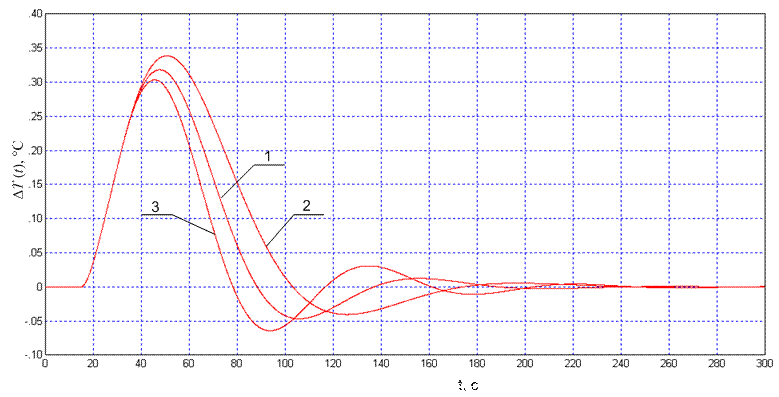1 - переходная характеристика с оптимальными параметрами; 2 - переходная характеристика с параметрами объекта увеличенными на 20%; 3 - переходная характеристика с параметрами объекта уменьшенными на 20%.

Рисунок 4.10 –  Проверка системы на грубость

Из рисунка 4.10 видно, что при изменении параметров регулятора качество процесса регулирования ухудшается, но при этом система остается устойчивой следовательно найденные параметры регулятора оптимальны.

Скачать файл