Общая постановка задачи оптимизации металлургических процессов, страница 9

то система называется сбалансированной. При выполнении условия баланса разумно накладывать такие ограничения на суммарный ввоз и вывоз груза, при которых полностью вывозится весь груз и не остается неудовлетворенных потребностей, т.е. условия (1) и (2) приобретают форму равенства. При таких ограничениях выполнение равенства (4) становится необходимым и достаточным условием для разрешимости транспортной задачи.

Специфическими для транспортной задачи являются следующие два обстоятельства: а) каждая из переменных  x_i,j  входит в два уравнения системы ограничений (1), (2); б) коэффициенты при переменных  x_i,j  в ограничениях равны единице. Благодаря этим особенностям симплекс-таблица состоит из нулей и единиц, что позволило разработать для решения транспортной задачи алгоритмы, существенно более простые, чем симплекс-метод.

Если спрос превышает предложение (или наоборот), то это приводит к дисбалансу. В этом случае вводят дополнительный фиктивный пункт поставщика (или потребителя), считая при этом, что каждая единица недопоставленной продукции облагается штрафом за недопоставку (за хранение).

Решение транспортной задачи включает два основных этапа: построение опорного решения (начального плана перевозок) и построение оптимального плана.

Для определения начального плана строится транспортная таблица, и используются правило северо-западного угла, метод минимального элемента или приближенный алгоритм Фогеля. Последние два метода предпочтительнее, т.к. дают результат, близкий к оптимальному.

Для построения оптимального решения применяют метод потенциалов (для нахождения вводимой в базис переменной) и построение цикла (для нахождения переменной, выводимой из базиса). Осуществляется итерационный процесс, на каждом шаге которого рассматривается некоторая текущая опорная точка, проверяется ее оптимальность и при необходимости определяется переход к “лучшей” опорной точке.

Пример. Имеются три пункта децентрализованного печатания газеты А, Б и В. Эти пункты должны обеспечить периодической печатью четыре области 1, 2, 3 и 4. Суточный выпуск газет в пунктах децентрализованного печатания a_А = 40, a_Б = 110 и a_В = 30 тысяч экземпляров. Потребность в газетах по каждой области: b₁ = 30; b₂ = 60; b₃ = 40; b ₄ = 50 тысяч экземпляров. Затраты на перевозку одной тысячи экземпляров газет в условных рублях задаются матрицей:

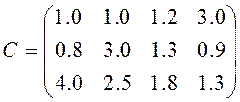
Составить такой план доставки газет, при котором суммарные затраты были бы минимальными.

Для решения задачи строится транспортная таблица. Найдем опорный план задачи методом северо-западного угла.

Затраты на перевозку газет по этому плану составят:

30×1,0 + 10×1,0 + 50×3,0 + 40×1,3 + 20×0,9 + 30×1,3 = 299

Однако этот план не оптимальный.

Каждое свободное место соответствует неизвестному, значение которого принято равным нулю, т.е. поездка не запланирована. Необходимо провести анализ того, имеется ли среди этих мест хотя бы одно такое, значение которого целесообразно принять больше нуля.

Включение в план соответствующей перевозки снизит транспортные расходы. Если ввести для свободного места единицу груза, то необходимо уменьшить на единицу какую-либо перевозку в соответствующем пункте отправления, чтобы остались выполненными ограничения задачи.