Общая постановка задачи оптимизации металлургических процессов, страница 5

Применяются при выборе оптимального плана и диеты, при организации ремонтных работ, при решении транспортных задач.

Постановка задачи

Найти такие переменные х₁^*, х₂^*, …, х_n^*, дающие экстремум функции

® extr

(1)

при ограничениях

xi ³ 0,

(2)

где i = 1, …, n – переменные; j = 1, …, m – ограничения.

Ограничения представляют собой систему линейных нестрогих неравенств, которые при необходимости могут быть преобразованы в равенства.

Свойства системы уравнений (2):

(1, 2) – выпуклые; (3, 4) – невыпуклые. Выпуклыми называются фигуры, которые содержат весь отрезок AB между двумя любыми точками, расположенными внутри фигуры. Вершины выпуклого многогранника R являются крайними точками. Если существует экстремум целевой функции, он является абсолютным и всегда является одной из крайних точек, либо отрезков.

Разработка моделей линейного программирования

Термин «разработка» означает построение моделей ЛП практических задач. Она включает следующие основные этапы:

-  определение переменных задачи;

-  представление ограничений задачи в виде линейных уравнений или неравенств;

-  задание линейной целевой функции, подлежащей минимизации или максимизации.

Например, завод по производству электронного оборудования выпускает два типа фильтров: нижних частот НЧ и полосовые П. на изготовление фильтров НЧ требуется две цифровые и пять аналоговых микросхем; на изготовление фильтров П – соответственно, пять и две. Еженедельный запас каждого вида микросхем составляет 10 000 штук. Имеется постоянный заказчик, которому завод поставляет 600 фильтров НЧ. Существует также профсоюзное соглашение, в соответствии с которым общее число производимых в течение одной недели изделий должно быть не меньше 1 500 штук. Производственные мощности позволяют выпускать максимум 2 250 фильтров НЧ и 1 750 фильтров полосовых. Для производства фильтров первого типа требуется 1 чел.-ч., для второго – 2 чел.-ч. Продолжительность рабочей недели 40 ч, число работающих 100 человек. Сколько фильтров каждого типа следует производить, чтобы максимизировать общий доход за неделю, если прибыль от производства одного фильтра НЧ составляет 30 руб., а от производства одного фильтра П – 40 руб. (2001г.)

Переменные x₁ и x₂ – количество произведенных за неделю фильтров НЧ и П соответственно, G общий доход за неделю. Тогда целевая функция будет иметь вид

G = 30x ₁ + 40x₂ ® max

Ограничения производственного процесса включают:

фонд рабочего времени                  x₁ + 2x₂ £ 4 000 (100 чел × 40 ч);

производственная мощность          x₁ £ 2 250; x₂ £ 1 750;

требуемое количество цифровых микросхем             2x₁ + 5x₂ £ 10 000;

                                     аналоговых микросхем           5x₁ + 2x₂ £ 10 000;

постоянные заказы                          x₁ ³ 600;

профсоюзное соглашение               x₁ + x₂ ³ 1 500;

условие неотрицательности           x₁ ³ 0, x₂ ³ 0.

Математическая модель задачи ЛП может быть представлена в одной из следующих форм: канонической; стандартной; общей.

Каноническая:

1.  Цель задачи: найти минимум

2.  Ограничения: уравнения

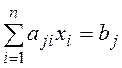
3.  Условия не отрицательности: все переменные x_i³ 0.

Стандартная:

1.  Цель задачи: найти максимум или минимум G(x_i)

2.  Ограничения: неравенства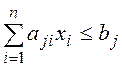

3.  Условия не отрицательности: все переменные x_i³ 0.

Общая:

1.  Цель задачи: найти максимум или минимум G(x_i)

2.  Ограничения: уравнения и неравенства

3.  Условия не отрицательности: часть переменных x_i³ 0.

Для применения типовых приемов решения задачи ЛП математическую модель записывают в канонической форме. Любую линейную модель можно привести к канонической следующим образом:

1)  Максимизация целевой функции G равносильна минимизации целевой функции –G.