Общая постановка задачи оптимизации металлургических процессов, страница 7

Смежное базисное решение отличается от рассматриваемого только одной базисной переменной. Для получения смежного допустимого базисного решения одну из базисных переменных превращают в небазисную и вводят одну из небазисных переменных в базис. Необходимо выбрать базисную и небазисную переменные так, чтобы замена одной из них на другую давала максимальное приращение G. Превращение небазисной переменной в базисную приводит к увеличению ее значения от нуля до некоторой положительной величины, поскольку в любом допустимом базисном решении базисные переменные положительны, а не базисные равны нулю.

Относительная оценка  позволяет определить изменения критерия G. Если  > 0, то можно добиться увеличения значения G (G>max). Если  < 0, то можно добиться уменьшения значения G (G<min).

Таким образом, если относительные оценки небазисных переменных допустимого базисного решения (для G > min) неотрицательны, то решение оптимально. В базис вводится небазисная переменная, имеющая наибольшую (по модулю) относительную оценку, т.е. имеет место наибольшее приращение целевой функции.

Если в оптимальном решении имеется небазисная переменная с нулевой относительной оценкой, то оптимальное решение не единственно.

Правило минимального отношения позволяет определить заменяемую базисную переменную. Предельному значению отвечает 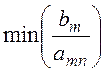 и базисная переменная x_n первой обращается в нуль. Строка, в которой находится заменяемая базисная переменная называется ведущей строкой, а коэффициент в ведущей строке при вводимой в базис переменной называется ведущим элементом.

Пример. Найти точку минимума функции          G = – 2x₁ – 4x₂

на допустимом множестве X, заданном ограничениями

3x₁ + 4x₂ £ 1 700,

2x₁ + 5x₂ £ 1 600,

x₁ ³ 0, x₂ ³ 0.

Приведем задачу к канонической форме:

G = – 2x₁ – 4x₂

x₁ ³ 0, x₂ ³ 0, x₃ ³ 0, x₄ ³ 0.

Поскольку правые части (1) положительны, а новые переменные x₃ и x₄ с единичными коэффициентами, то полученное решение x₁ = 0, x₂ = 0, x₃ = 1 700, x₄ = 1 600 образует опорную точку (допустимое базисное решение). Переменные x₃ и x₄ являются базисными, а x₁ и x₂ – не базисными. Целевая функция и ограничения выражены через небазисные переменные.

Т.к. коэффициенты целевой функции отрицательны, необходимо перейти к смежному допустимому базисному решению. В качестве новой базисной переменной принимаем x₂, поскольку эта небазисная переменная имеет наибольшую (по модулю) относительную оценку (коэффициент).

Определяем минимум отношений правых частей уравнений к коэффициентам при x₂:

.

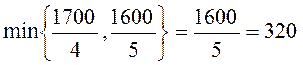Он достигается в уравнении, содержащем базисную переменную x₄, поэтому она выводится из базиса, а уравнение является ведущим (или разрешающим).

Базисными переменными теперь являются x₂ и x₃, а небазисными – x₁ и x₄.

Выражаем ограничения и целевую функцию через небазисные переменные.

Ведущее уравнение: .

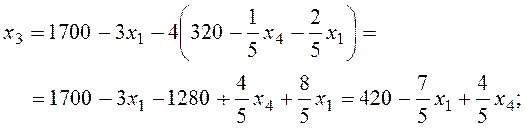
Новая опорная точка: x₁ = 0, x₂ = 320, x₃ = 420, x₄ = 0. G = – 1 280.

Переменная x₁ входит в выражение целевой функции с отрицательным коэффициентом, оптимальное решение еще не достигнуто, поэтому переходим к следующей опорной точке. Переменную x₁ вводим в базис.

Определяем минимум отношений правых частей уравнений к коэффициентам при x₁:

.

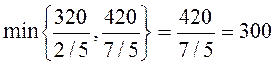Он достигается в уравнении, содержащем базисную переменную x₃, поэтому она выводится из базиса, а уравнение является ведущим.

В новый список базисных переменных теперь входят x₁ и x₂, а небазисными переменными являются x₃ и x₄.

Выражаем ограничения и целевую функцию через небазисные переменные.

Ведущее уравнение: .

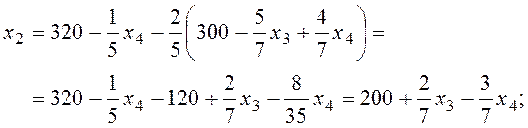
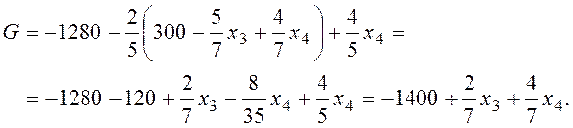
Новая опорная точка: x₁ = 300, x₂ = 200, x₃ = 0, x₄ = 0. G = – 1 400.

Изменение значения любой из небазисных переменных x₃, x₄ (эти переменные входят в целевую функцию с положительными коэффициентами) приведет к возрастанию значения целевой функции. Таким образом, дальнейшее убывание целевой функции невозможно, ее минимальное значение G_min = – 1400 достигнуто в точке x₁ = 300, x₂ = 200.