Общая постановка задачи оптимизации металлургических процессов, страница 6

2)  Исходное ограничение, записанное в виде неравенства типа £ или ³, можно представить в виде равенства, прибавляя или вычитая дополнительную неотрицательную переменную к левой части ограничения. Число таких переменных равно числу неравенств в системе ограничений. (Чтобы дополнительные переменные не оказывали влияние на значение целевой функции, они должны входить в целевую функцию с нулевыми коэффициентами.)

3)  Если переменная x_i не имеет ограничений в знаке, то она заменяется разностью двух неотрицательных переменных:

x_i = x_i¢ – x_i¢¢, x_i¢ ³ 0, x_i¢¢ ³ 0.

Таким образом, преобразование задачи в каноническую форму приводит к увеличению размерности задачи (количества переменных).

Графический способ решения задач линейного программирования

Постановка задачи: минимизировать G = 40x₁ + 36x₂ при ограничениях

Геометрически сочетание всех неравенств дает многоугольную область, называемую допустимым множеством (областью) решений. Она получается в результате пересечения всех полуплоскостей, отвечающих неравенствам системы. Оптимальное решение, т.е. лучшее допустимое решение, всегда находится на границе допустимой области изменения переменных: либо в одной из ее вершин, либо на грани, либо при наличии незамкнутой области имеет бесконечно большое значение.

Из линейности целевой функции следует, что ее градиент – вектор, указывающий направление возрастания функции и перпендикулярный ей, 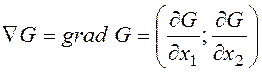 постоянен в любой точке, а линии уровня функции G параллельны друг другу.

Симплекс-метод решения задач линейного программирования

Использование графического способа удобно только при решении задач ЛП с двумя переменными. При большем числе переменных необходимо применение алгебраического аппарата. Симплекс-метод является общим методом решения задач ЛП, с помощью которого можно получить экономическую интерпретацию полученного решения и провести анализ модели на чувствительность. Решение находится с помощью итеративной процедуры.

Классическим методом решения систем линейных уравнений является метод Гаусса-Жордана. Он заключается в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над

Переменные х₁, х₂, …, х_m, входящие с единичными коэффициентами, называются базисными или зависимыми. Остальные переменные – небазисные.

Базисным решением системы в каноническом виде называется решение, полученное при нулевых значениях небазисных переменных (х₁ = b₁,…, х_m = b_m, х_m+1 = … = х_n =0).

Если b₁ ³ 0, …, b_m ³ 0, то полученное решение называется допустимым базисным решением.

Основная идея симплекс-метода заключается в упорядоченном переборе базисных допустимых решений, при котором осуществляется переход от текущей опорной точки (базисного допустимого решения) только к тем опорным точкам, в которых значение целевой функции меньше, чем в текущей.

Алгоритм симплекс-метода включает следующие основные шаги:

-  сведение задачи ЛП к каноническому виду;

-  выбор допустимого базисного решения;

-  выражение ограничений и целевой функции через небазисные переменные (переменные, равные нулю в точке решения);

-  если коэффициенты целевой функции (при небазисных переменных) отрицательны (задача нахождения минимума), необходимо перейти к смежному допустимому базисному решению с меньшим значением целевой функции, и возвратиться к предыдущему пункту; если коэффициенты целевой функции положительны, точка оптимума найдена.