1. Последовательность этапов реализации оптимизационной задачи в порядке их выполнения:
а) проверка задачи на существование и единственность решения
б) моделирование рассматриваемой физической ситуации
в) анализ результата и интерполяция его в терминах физического содержания модели
г) выбор подходящей математической процедуры для осуществления оптимизации
д) реализация выбранной процедуры на практике
(Эталон: б; а; г; д; в)
2. Минимизируемая функция f(x) называется _________.
(Эталон: целевая, целевой)
3. Методы, используемые для решения задач, в которых критерий оптимизации представляется в виде функционалов, называются методами _________ оптимизации.
(Эталон: динамической)
4. Метод оптимизации, в котором осуществляется переход задачи с ограничениями к задаче без ограничений – метод …
а) классического анализа
б) множителей Лагранжа
в) линейного программирования
г) нелинейного программирования
(Эталон: б)
5. Достаточные условия существования экстремума функции:
а) G(xk–e) > G(xk+e) > G(xk)
б) G(xk–e) > G(xk) > G(xk+e)
в) G¢ (xk–e) > 0, G¢ (xk+e) > 0
г) G¢ (xk–e) < 0, G¢ (xk+e) > 0
д) G¢¢ (xk) < 0
(Эталон: а; г; д)
6. Решение задачи f(x) = -x4 + 3x2 ® min, x Î R, согласно необходимым и достаточным условиям оптимальности – точка х = …
а) -1
б) 0
в) 1
г) ![]()
д) ![]()
(Эталон: б)
7. Следующий отрезок локализации минимума внутри отрезка [0, 2] при f(0.7) = -0.35, f(1.3) = -0.42 – …
а) [0, 0.7]
б) [0, 1.3]
в) [0.7, 1.3]
г) [0.7, 2]
д) [1.3, 2]
(Эталон: г)
8. Характеристика точки x=4 на графике функции …
|
а) строгого локального минимума б) нестрогого локального максимума в) нестрогого глобального минимума г) строгого глобального минимума |
|
(Эталон: в)
9. Форма
задачи линейного программирования 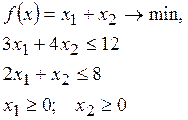 – …
– …
а) каноническая
б) общая
в) основная
г) двойственная
д) стандартная
(Эталон: д)
10. Вид ограничений общей задачи линейного программирования – …
а) уравнения и неравенства
б) только уравнения
в) только неравенства
г) только условия неотрицательности
(Эталон: а)
11. Вид
задачи линейного программирования 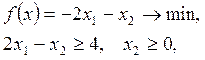 в канонической форме –
…
в канонической форме –
…
а) ![]()
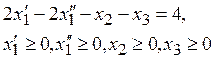
б) ![]()
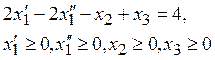
в) ![]()
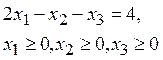
г) ![]()
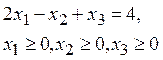
(Эталон: а)
12. Опорная
точка допустимого множества 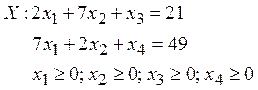 – …
– …
а) (1, 2, 0, 0)
б) (5, 1, 4, 12)
в) (0, 0, 21, 49)
г) (0, 3, 0, 0)
д) (5, 0, 11, 14)
(Эталон: в)
13. Соответствие точки ее типу:
|
1) A 2) B 3) C 4) D |
а) узловая б) крайняя в) граничная г) внутренняя д) особая е) недопустимая |
|
(Эталон: 1 – г; 2 – б; 3 – в; 4 – е)
14. Этапы построения модели линейного программирования:
а) определение переменных задачи
б) сбор статистических данных
в) расчет плотности распределения
г) представление ограничений в виде уравнений или неравенств
д) задание целевой функции
(Эталон: а; г; д)
15. Транспортную задачу всегда можно…
а) отрегулировать
б) сбалансировать
в) уравновесить
г) выровнять
д) состыковать
(Эталон: б)
16. Методы нулевого порядка:
а) дихотомии
б) наискорейшего спуска
в) релаксации
г) наилучшей пробы
д) Фибоначчи
(Эталон: а; г; д)
17. Критерий оптимальности в задачах динамической оптимизации – _________.
(Эталон: функционал)
1. Последовательность этапов в методах исключения интервала в порядке их выполнения:
а) вычисляем x1 и x2
б) вычисляем е=f(x1) – f(x2)
в) задаем точность e
г) проверяем условие окончания счета
д) выбираем следующий отрезок
(Эталон: в; а; б; д; г)
2. Свойство непрерывной функции, характеризующее наличие у нее одной точки минимума на отрезке [a,b] – _________.
(Эталон: унимодальность)
3. Необходимым условием оптимальности в задаче безусловной оптимизации является равенство нулю _________ функции.
(Эталон: градиента, производной)
4. Класс
задач оптимизации, к которым относится задача: ![]()
![]()
![]() – … оптимизация.
– … оптимизация.
а) безусловная
б) линейная
в) нелинейная
г) дискретная
д) динамическая
(Эталон: б)
5. Достаточные условия существования экстремума функции:
а) G(xk–e) < G(xk) < G(xk+e)
б) G(xk–e) < G(xk+e) < G(xk)
в) G¢ (xk–e) > 0, G¢ (xk+e) < 0
г) G¢ (xk–e) < 0, G¢ (xk+e) < 0
д) G¢¢ (xk) = 0, G (3) (xk) > 0
(Эталон: б; в)
6. Решение задачи f(x) = x3 + 3x2 ® min, x Î R, согласно необходимым и достаточным условиям оптимальности – точка х = …
а) -4
б) -2
в) 0
г) 2
д) 4
(Эталон: в)
7. Следующий отрезок локализации минимума внутри отрезка [-1, 0] при f(-0.6) = 0.2, f(-0.4) = 0.5 – …
а) [-1, -0.6]
б) [-1, -0.4]
в) [-0.6, -0.4]
г) [-0.6, 0]
д) [-0.4, 0]
(Эталон: б)
8. Характеристика точки x=1,3 приведена на графике функции …
|
а) строгого локального максимума б) нестрогого локального максимума в) строгого локального минимума г) нестрогого глобального максимума |
|
(Эталон: г)
9. Форма
задачи линейного программирования 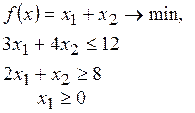 – …
– …
а) каноническая
б) общая
в) основная
г) двойственная
д) стандартная
(Эталон: б)
10. Операции,
необходимые для преобразования ограничения ![]() к каноническому
виду:
к каноническому
виду:
а) добавления новой переменной со знаком плюс
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.