а) 
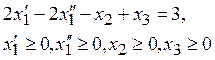
б) 
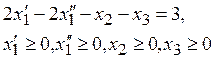
в) 
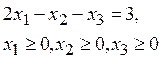
г) 
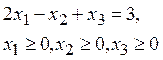
(Эталон: а)
12. Опорная
точка допустимого множества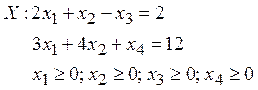 
– …
а) (1, 0, 0, 9)
б) (1, 1, 0, 0)
в) (1, 1, 1, 5)
г) (1, 0, 1, 1)
д) (0, 3, 0, 0)
(Эталон: а)
13. Соответствие точки ее типу:
|
1) A 2) B 3) C 4) D |
а) узловая б) крайняя в) граничная г) внутренняя д) особая е) недопустимая |
|
(Эталон: 1 – в; 2 – е; 3 – г; 4 – б)
14. Содержательный смысл целевой функции в задаче производственного планирования на максимум…
а) себестоимость
б) мощность
в) сырье
г) прибыль
(Эталон: г)
15. Метод, которым может быть решена транспортная задача, – …
а) симплексный
б) градиентный
в) золотого сечения
г) случайный
д) Фибоначчи
(Эталон: а)
16. Методы многомерной оптимизации:
а) дихотомии
б) наискорейшего спуска
в) релаксации
г) наилучшей пробы
д) Фибоначчи
(Эталон: б; в)
17. Дифференциальное уравнение, которым записываются необходимые и достаточные условия при решении задачи динамического программирования, называется уравнением _________.
(Эталон: Беллмана)
1. Последовательность этапов в методах исключения интервала в порядке их выполнения:
а) вычисляем x1 и x2
б) задаем точность e
в) выбираем следующий отрезок
г) сравниваем f(x1) и f(x2)
д) проверяем условие окончания счета
(Эталон: б; а; г; в; д)
2. Отличие
мономодальных от мультимодальных функций состоит в
количестве _________.
(Эталон: экстремумов)
3. Достаточное условие оптимальности в задаче безусловной оптимизации связано с производными функции _________ порядка.
(Эталон: второго; второй)
4. Условия оптимальности бывают:
а) глобальные
б) локальные
в) необходимые
г) достаточные
д) качественные
(Эталон: в, г)
5. Достаточные условия существования экстремума функции:
а) G(xk–e) > G(xk) < G(xk+e)
б) G(xk–e) < G(xk+e) < G(xk)
в) G¢¢ (xk) = G (3) (xk) = 0, G(4) (xk) < 0
г) G¢ (xk–e) < 0, G¢ (xk+e) < 0
д) G¢ (xk–e) < 0, G¢ (xk+e) > 0
(Эталон: а; в; д)
6. Решение задачи f(x) = x3 - 3x2 ® min, x Î R, согласно необходимым и достаточным условиям оптимальности – точка х = …
а) -2
б) -0.5
в) 0
г) 2
д) 3
(Эталон: г)
7. Следующий отрезок локализации минимума внутри отрезка [2, 3] f(2.3) = 0.35, f(2.7) = -0.4 – …
а) [2, 2.3]
б) [2, 2.7]
в) [2.3, 2.7]
г) [2.3, 3]
д) [2.7, 3]
(Эталон: г)
8. Характеристика точки x=0 приведена на графике функции …
|
а) строгого локального максимума б) нестрогого локального максимума в) строгого глобального минимума г) нестрогого глобального максимума |
|
(Эталон: в)
9. Задача
минимизации линейного программирования на множестве Х с ограничениями типа 
называется …
а) каноническая
б) основная
в) общая
г) двойственная
д) стандартная
(Эталон: а)
10. Операции,
необходимые для преобразования ограничения 
, где x1≥0, к каноническому виду:
а) добавления новой переменной со знаком плюс
б) добавления новой переменной со знаком минус
в) замена знака неравенства на равенство
г) замена знака неравенства на противоположный
д) замена переменной x2 разностью двух переменных
(Эталон: б; в; д)
11. Вид
задачи линейного программирования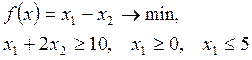 
в канонической форме –
…
а) 
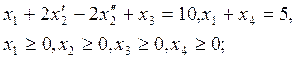
б) 
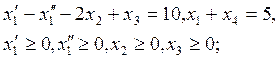
в) 
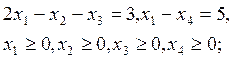
г) 
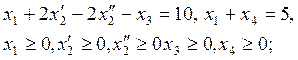
(Эталон: г)
12. Опорная
точка допустимого множества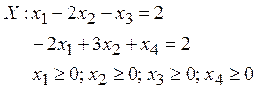 
– …
а) (3, 0, 1, 8)
б) (2, 0, 0, 6)
в) (0, 0, 2, 2)
г) (3, 1, 0, 5)
д) (4, 0, 0, 10)
(Эталон: б)
13. Соответствие точки ее типу:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
